Difference between revisions of "Manuals/calci/DB"
Jump to navigation
Jump to search
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | =DB( | + | <div style="font-size:30px">'''DB (Cost,Salvage,Life,Period,NoMonths)'''</div><br/> |
| − | |||
Where | Where | ||
| − | *<math> | + | *<math>Cost</math> is the initial cost of an asset, |
*<math>Salvage</math> is the value at the end of depreciation, | *<math>Salvage</math> is the value at the end of depreciation, | ||
| − | *<math> | + | *<math>Life</math> is life of an asset that indicates the number of periods over which the asset is being depreciated, |
| − | *<math> | + | *<math>Period</math> is the period for which depreciation is to be calculated, and |
*<math>NoMonths</math> specifies how many months of the year are used in the calculation of the first period of depreciation. | *<math>NoMonths</math> specifies how many months of the year are used in the calculation of the first period of depreciation. | ||
| − | + | **DB(), returns the depreciation of an asset for a specified period by using the fixed-declining balance method. | |
| − | DB() | ||
== Description == | == Description == | ||
| − | DB( | + | DB (Cost,Salvage,Life,Period,NoMonths) |
*Depreciation is the decrease in value of assets. Depreciation of an asset is highest in the first period and decreases in successive periods. | *Depreciation is the decrease in value of assets. Depreciation of an asset is highest in the first period and decreases in successive periods. | ||
*DB() calculates the depreciation using the fixed-declining balance method. | *DB() calculates the depreciation using the fixed-declining balance method. | ||
*If <math>Salvage</math> <0, Calci displays #N/A error message. | *If <math>Salvage</math> <0, Calci displays #N/A error message. | ||
| − | *If <math> | + | *If <math>Cost</math> ,<math>L</math>, <math>P</math>, <math>NoMonths</math> <=0, Calci displays #N/A error message. |
| − | *If <math> | + | *If <math>Period</math> is not an integer, Calci rounds up the value (e.g. 4.2 is rounded up to 5). |
== Examples == | == Examples == | ||
Latest revision as of 16:04, 22 August 2018
DB (Cost,Salvage,Life,Period,NoMonths)
Where
- is the initial cost of an asset,
- is the value at the end of depreciation,
- is life of an asset that indicates the number of periods over which the asset is being depreciated,
- is the period for which depreciation is to be calculated, and
- specifies how many months of the year are used in the calculation of the first period of depreciation.
- DB(), returns the depreciation of an asset for a specified period by using the fixed-declining balance method.
Description
DB (Cost,Salvage,Life,Period,NoMonths)
- Depreciation is the decrease in value of assets. Depreciation of an asset is highest in the first period and decreases in successive periods.
- DB() calculates the depreciation using the fixed-declining balance method.
- If <0, Calci displays #N/A error message.
- If ,, , <=0, Calci displays #N/A error message.
- If is not an integer, Calci rounds up the value (e.g. 4.2 is rounded up to 5).
Examples
1. =DB(20000,2000,5,4.5,2) : This example is used to find the yearly depreciation of an asset that costs $20,000 at the start of year 4.5, and has a salvage value of $2,000 after 5 years. The depreciation calculation starts 2 months into year 1.
Displays 2,757.7148 as a result.
2. =DB(10000,1000,5,1,6) : This example is used to find the yearly depreciation of an asset that costs $10,000 at the start of year 1, and has a salvage value of $1,000 after 5 years. The depreciation calculation starts 6 months into year 1.
Displays 1,845.00 as a result.
Related Videos
See Also
References
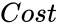 is the initial cost of an asset,
is the initial cost of an asset, is the value at the end of depreciation,
is the value at the end of depreciation,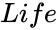 is life of an asset that indicates the number of periods over which the asset is being depreciated,
is life of an asset that indicates the number of periods over which the asset is being depreciated,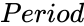 is the period for which depreciation is to be calculated, and
is the period for which depreciation is to be calculated, and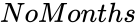 specifies how many months of the year are used in the calculation of the first period of depreciation.
specifies how many months of the year are used in the calculation of the first period of depreciation.
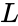 ,
, 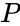 ,
,