Difference between revisions of "Manuals/calci/BINOMIALCOEFFICIENT"
Jump to navigation
Jump to search
(Created page with "==BInomial==") |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:30px">'''BINOMIAL(N,K)'''</div><br/> |
| + | *<math>N</math> is the number of items. | ||
| + | *<math>K </math> is the number of selection. | ||
| + | |||
| + | |||
| + | ==Description== | ||
| + | *This function gives the coefficent of the binomial distribution. | ||
| + | *Binomial coefficient is the set of positive integer which equals the number of combinations of k items that can be selected from a set of n items. | ||
| + | *The coefficients satisfy the Pascals recurrence. | ||
| + | *The binomial coefficents are denoted by <math>\binom{n}{k}</math> and it is read by n choose k. | ||
| + | *It is the coefficient of the <math>x^k</math> term in the polynomial expansion of the binomial thorem <math>(1 + x)^n</math>. | ||
| + | *The coefficient is occur in the formula of binomial thorem: | ||
| + | <math>(x+y)^n=\sum _{k=0}^n \binom{n}{k} x^{n-k} y^k</math> where <math> k\le n</math>. | ||
| + | *To find the coefficient of the binomial ,we can use several methods. | ||
| + | 1. Recursive formula | ||
| + | 2. Multiplicative formula | ||
| + | 3. Factorial formula. | ||
| + | *1.Recursive Formula: | ||
| + | <math>\binom{n}{k}= \binom{n-1}{k-1} +\binom{n-1}{k}</math> for <math>n,k>0</math> and <math>1\le k\le n-1</math>. | ||
| + | *2. Multiplicative formula: | ||
| + | <math>\binom{n}{k}= \prod_{i=1}^k \frac{n+1-i}{i}</math> | ||
| + | *3.Factorial formula: | ||
| + | <math>\binom{n}{k}= \frac{n!}{k!(n-k)!}</math> where <math>k\le n</math>,and which is zero when <math>k>n</math>. | ||
| + | *Also for the initial values <math> \binom{n}{0}=\binom{n}{n}=1 </math> for <math>n\ge 0</math>. | ||
| + | *Most compact formula for the coefficient of the binomial value is Factorial formula. | ||
| + | *Factorial formula is symmetric of the combination formula. | ||
| + | |||
| + | |||
| + | ==Examples== | ||
| + | #=BINOMIAL(10,3)= 120 | ||
| + | #=BINOMIAL(32,0)= 1 | ||
| + | #=BINOMIAL(10,7) = 120 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=07oNEAcZNko|280|center|Binomial coefficient}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/BINOMDIST | BINOMDIST ]] | ||
| + | *[[Manuals/calci/BINOMDIST | BINOMIALDIST ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Binomial_distribution Binomial Distribution] | ||
| + | *[http://en.wikipedia.org/wiki/Binomial_coefficient Binomial Coefficient] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:46, 27 November 2018
BINOMIAL(N,K)
- is the number of items.
- is the number of selection.
Description
- This function gives the coefficent of the binomial distribution.
- Binomial coefficient is the set of positive integer which equals the number of combinations of k items that can be selected from a set of n items.
- The coefficients satisfy the Pascals recurrence.
- The binomial coefficents are denoted by and it is read by n choose k.
- It is the coefficient of the term in the polynomial expansion of the binomial thorem .
- The coefficient is occur in the formula of binomial thorem:
where .
- To find the coefficient of the binomial ,we can use several methods.
1. Recursive formula 2. Multiplicative formula 3. Factorial formula.
- 1.Recursive Formula:
for and .
- 2. Multiplicative formula:
- 3.Factorial formula:
where ,and which is zero when .
- Also for the initial values for .
- Most compact formula for the coefficient of the binomial value is Factorial formula.
- Factorial formula is symmetric of the combination formula.
Examples
- =BINOMIAL(10,3)= 120
- =BINOMIAL(32,0)= 1
- =BINOMIAL(10,7) = 120
Related Videos
See Also
References
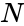 is the number of items.
is the number of items.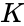 is the number of selection.
is the number of selection.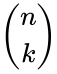 and it is read by n choose k.
and it is read by n choose k.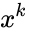 term in the polynomial expansion of the binomial thorem
term in the polynomial expansion of the binomial thorem 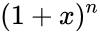 .
.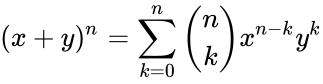 where
where 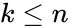 .
.
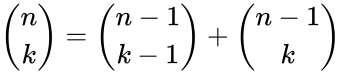 for
for 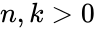 and
and  .
.
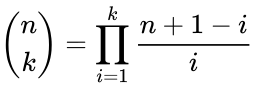
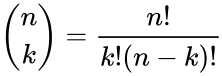 where
where 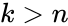 .
.
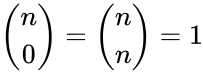 for
for 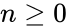 .
.