Difference between revisions of "Manuals/calci/CARTESIANPRODUCT"
Jump to navigation
Jump to search
| (6 intermediate revisions by 2 users not shown) | |||
| Line 9: | Line 9: | ||
*Consider two sets <math>\llcorner A </math> and <math>\llcorner B </math>. | *Consider two sets <math>\llcorner A </math> and <math>\llcorner B </math>. | ||
*The Cartesian product of <math>\llcorner A </math> and <math>\llcorner B </math> are denoted by <math>\llcorner AXB </math> is the set of all ordered pairs <math>\llcorner (a,b) </math> such that <math>a \in A</math> and <math>b \in B</math>. | *The Cartesian product of <math>\llcorner A </math> and <math>\llcorner B </math> are denoted by <math>\llcorner AXB </math> is the set of all ordered pairs <math>\llcorner (a,b) </math> such that <math>a \in A</math> and <math>b \in B</math>. | ||
| − | <math>\llcorner A </math> | + | <math>\llcorner AXB</math> = {<math>(a,b)|a \in A,b \in B</math>} |
| + | |||
| + | ==Examples== | ||
| + | 1.CARTESIANPRODUCT([2,4,6],[10,13,7]) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 2 || 10 | ||
| + | |- | ||
| + | | 2|| 13 | ||
| + | |- | ||
| + | | 2 || 7 | ||
| + | |- | ||
| + | | 4 || 10 | ||
| + | |- | ||
| + | | 4 || 13 | ||
| + | |- | ||
| + | | 4 || 7 | ||
| + | |- | ||
| + | | 6 || 10 | ||
| + | |- | ||
| + | | 6 || 13 | ||
| + | |- | ||
| + | | 6 || 7 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=NnEkVooAsxk|280|center|CARTESIAN PRODUCT}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/DOTPRODUCT | DOTPRODUCT ]] | ||
| + | *[[Manuals/calci/CROSSPRODUCT | CROSSPRODUCT ]] | ||
==References== | ==References== | ||
[http://ndp.jct.ac.il/tutorials/discrete/node28.html Cartesian Product] | [http://ndp.jct.ac.il/tutorials/discrete/node28.html Cartesian Product] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:54, 10 December 2018
CARTESIANPRODUCT (GivenSet1,GivenSet2)
- and are the set of numbers to find product.
Description
- This function shows the Cartesian product of two sets.
- Cartesian product is the product of two sets.
- The product of set X and set Y is the set that contains all ordered pairs ( x, y ) for which x belongs to X and y belongs to Y.
- In , and are two set of real numbers with a pair of numbers.
- Consider two sets and .
- The Cartesian product of and are denoted by is the set of all ordered pairs such that and .
= {}
Examples
1.CARTESIANPRODUCT([2,4,6],[10,13,7])
| 2 | 10 |
| 2 | 13 |
| 2 | 7 |
| 4 | 10 |
| 4 | 13 |
| 4 | 7 |
| 6 | 10 |
| 6 | 13 |
| 6 | 7 |
Related Videos
See Also
References
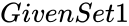 and
and 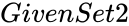 are the set of numbers to find product.
are the set of numbers to find product.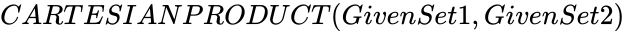 ,
,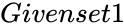 and
and 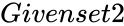 are two set of real numbers with a pair of numbers.
are two set of real numbers with a pair of numbers.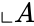 and
and 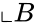 .
.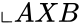 is the set of all ordered pairs
is the set of all ordered pairs 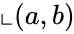 such that
such that 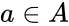 and
and 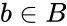 .
.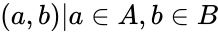 }
}