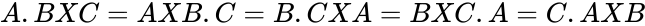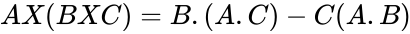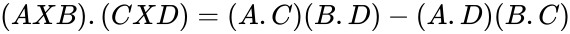Difference between revisions of "Manuals/calci/DYADIC"
Jump to navigation
Jump to search
| (10 intermediate revisions by 2 users not shown) | |||
| Line 8: | Line 8: | ||
*In <math>VECTORDIRECTPRODUCT (a,b)</math>, <math>a</math> and <math>b</math> are the two vectors. | *In <math>VECTORDIRECTPRODUCT (a,b)</math>, <math>a</math> and <math>b</math> are the two vectors. | ||
*Multiplying one vector by another under the direct product gives a tensor result. | *Multiplying one vector by another under the direct product gives a tensor result. | ||
| − | *The rectangular components of the direct product may be found by matrix multiplication: one multiplies the column vector A by the transpose of B, which gives a 3X3 matrix:<math>AB=AB^T</math>= | + | *The rectangular components of the direct product may be found by matrix multiplication: one multiplies the column vector A by the transpose of B, which gives a 3X3 matrix: |
| + | <math>AB=AB^T</math>= | ||
<math>\begin{pmatrix} | <math>\begin{pmatrix} | ||
A_x \\ | A_x \\ | ||
A_y \\ | A_y \\ | ||
A_z | A_z | ||
| − | \end{pmatrix}</math> | + | \end{pmatrix}</math><math> (B_x B_y B_Z)</math>=<math>\begin{pmatrix} |
| − | *The direct product is non-commutative (AB | + | A_xB_x & A_xB_y & A_xB_z \\ |
| + | A_yB_x & A_yB_y & A_yB_z \\ | ||
| + | A_z B_x &A_zB_y & A_zB_z | ||
| + | \end{pmatrix}</math> | ||
| + | *The direct product is non-commutative <math>(AB \neq BA)</math>. | ||
| + | *A few vector product identities are of interest: | ||
| + | #<math>A.BXC = AXB.C=B.CXA=BXC.A=C.AXB</math> | ||
| + | #<math>AX(BXC)= B.(A.C)- C(A.B)</math> | ||
| + | #<math>(AXB)XC = B(A.C)-A(B.C)</math> | ||
| + | #<math>(AXB).(CXD)= (A.C)(B.D)-(A.D)(B.C)</math> | ||
| + | #<math>(AXB).(CXD) = (AxB.D)C-(AxB.C)D</math> | ||
| + | |||
| + | ==Examples== | ||
| + | #DYADIC([1,2,3],[8,7,6]) = 40 | ||
| + | #VECTORDIRECTPRODUCT([14,17,20],[22,26,5]) = 850 | ||
| + | #VECTORDIRECTPRODUCT([2.7,3.9,10.2],[14.5,19,-4]) = 72.45 | ||
| + | #DYADIC([-8,-4,2],[10,-45,67]) = 234 | ||
| + | |||
| + | ==Related Videos== | ||
| + | {{#ev:youtube|v=tpL95Sd7zT0|280|center|Tensor Product}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/DOTPRODUCT | DOTPRODUCT ]] | ||
| + | *[[Manuals/calci/CROSSPRODUCT | CROSSPRODUCT ]] | ||
| + | *[[Manuals/calci/CARTESIANPRODUCT | CARTESIANPRODUCT ]] | ||
| + | |||
| + | ==References== | ||
| + | [http://www.pgccphy.net/ref/vprod.pdf Direct Product] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:41, 10 January 2019
DYADIC(a,b)
OR VECTORDIRECTPRODUCT (a,b)
- and any two set of values.
Description
- This function shows the Vector Direct product.
- The third type of vector multiplication is called the direct product, and is written AB.
- In , and are the two vectors.
- Multiplying one vector by another under the direct product gives a tensor result.
- The rectangular components of the direct product may be found by matrix multiplication: one multiplies the column vector A by the transpose of B, which gives a 3X3 matrix:
= =
- The direct product is non-commutative .
- A few vector product identities are of interest:
Examples
- DYADIC([1,2,3],[8,7,6]) = 40
- VECTORDIRECTPRODUCT([14,17,20],[22,26,5]) = 850
- VECTORDIRECTPRODUCT([2.7,3.9,10.2],[14.5,19,-4]) = 72.45
- DYADIC([-8,-4,2],[10,-45,67]) = 234
Related Videos
See Also
References
 and
and 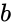 any two set of values.
any two set of values.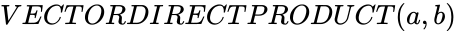 ,
, 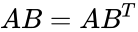 =
=
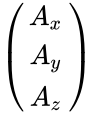
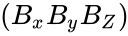 =
=
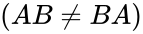 .
.