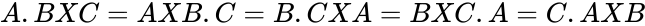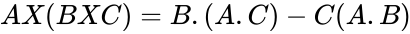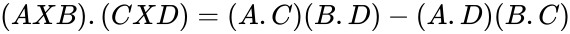Difference between revisions of "Manuals/calci/DYADIC"
Jump to navigation
Jump to search
| Line 32: | Line 32: | ||
#VECTORDIRECTPRODUCT([2.7,3.9,10.2],[14.5,19,-4]) = 72.45 | #VECTORDIRECTPRODUCT([2.7,3.9,10.2],[14.5,19,-4]) = 72.45 | ||
#DYADIC([-8,-4,2],[10,-45,67]) = 234 | #DYADIC([-8,-4,2],[10,-45,67]) = 234 | ||
| + | |||
| + | ==Related Videos== | ||
| + | {{#ev:youtube|v=tpL95Sd7zT0|280|center|Tensor Product}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 15:41, 10 January 2019
DYADIC(a,b)
OR VECTORDIRECTPRODUCT (a,b)
- and any two set of values.
Description
- This function shows the Vector Direct product.
- The third type of vector multiplication is called the direct product, and is written AB.
- In , and are the two vectors.
- Multiplying one vector by another under the direct product gives a tensor result.
- The rectangular components of the direct product may be found by matrix multiplication: one multiplies the column vector A by the transpose of B, which gives a 3X3 matrix:
= =
- The direct product is non-commutative .
- A few vector product identities are of interest:
Examples
- DYADIC([1,2,3],[8,7,6]) = 40
- VECTORDIRECTPRODUCT([14,17,20],[22,26,5]) = 850
- VECTORDIRECTPRODUCT([2.7,3.9,10.2],[14.5,19,-4]) = 72.45
- DYADIC([-8,-4,2],[10,-45,67]) = 234
Related Videos
See Also
References
 and
and 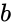 any two set of values.
any two set of values.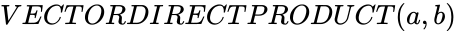 ,
, 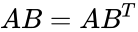 =
=
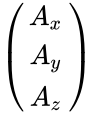
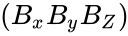 =
=
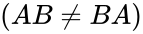 .
.