Difference between revisions of "Manuals/calci/EXPOF"
Jump to navigation
Jump to search
(Created page with "expof") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <div style="font-size:30px">'''EXPOF(x)'''</div><br/> | |
| + | *<math>x</math> is the number. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the <math>e</math> raised to the power of number. | ||
| + | *In <math>EXPOF(x)</math>, where <math>x</math> represents the exponent of <math>e</math> or <math>e^x</math>. | ||
| + | *The approximate value of the constant <math>e=2.718281828459045</math> and it is equal to <math>e^x</math> or <math>EXP(1)</math>. | ||
| + | *It is called the Mathematical Constant or Euler's Number or Napier's Constant. | ||
| + | *It is the base of natural logarithm. | ||
| + | *It can be calculate the sum of infinite series: <math>e=1+\frac{1}{1}+\frac{1}{1.2}+\frac{1}{1.2.3}+\frac{1}{1.2.3.4} +...</math> | ||
| + | *And the inverse function of the natural logarithm function is the exponential function: | ||
| + | <math>f^{-1}(x) = e^x</math>. | ||
| + | |||
| + | ==Examples== | ||
| + | #EXPOF(3) = 2.718281828459045 7.38905609893065 20.085536923187668 | ||
| + | #EXPOF(5.2) = 2.718281828459045 7.3890560989306495 20.085536923187664 54.59815003314423 148.41315910257657 | ||
| + | #EXPOF(7/3) = 2.718281828459045 7.3890560989306495 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=T3zzvj6wSCQ|280|center|EXP Function}} | ||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | *[[Manuals/calci/IMEXP | IMEXP ]] | ||
| + | *[[Manuals/calci/LOG | LOG ]] | ||
| + | *[[Manuals/calci/LN | LN ]] | ||
| + | |||
| + | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Exponential_function Exponential function] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:57, 11 January 2019
EXPOF(x)
- is the number.
Description
- This function gives the raised to the power of number.
- In , where represents the exponent of or .
- The approximate value of the constant and it is equal to or .
- It is called the Mathematical Constant or Euler's Number or Napier's Constant.
- It is the base of natural logarithm.
- It can be calculate the sum of infinite series:
- And the inverse function of the natural logarithm function is the exponential function:
.
Examples
- EXPOF(3) = 2.718281828459045 7.38905609893065 20.085536923187668
- EXPOF(5.2) = 2.718281828459045 7.3890560989306495 20.085536923187664 54.59815003314423 148.41315910257657
- EXPOF(7/3) = 2.718281828459045 7.3890560989306495
 is the number.
is the number.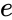 raised to the power of number.
raised to the power of number.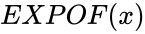 , where
, where 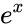 .
.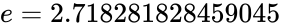 and it is equal to
and it is equal to 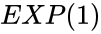 .
.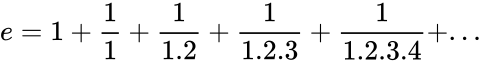
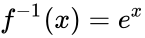 .
.