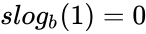Difference between revisions of "Manuals/calci/SUPERLOGARITHM"
Jump to navigation
Jump to search
| (One intermediate revision by the same user not shown) | |||
| Line 14: | Line 14: | ||
<math>slog_{b}(b^{z}) = slog_{b}{z}+1 </math> and | <math>slog_{b}(b^{z}) = slog_{b}{z}+1 </math> and | ||
<math> slog_{b}(1) = 0</math> | <math> slog_{b}(1) = 0</math> | ||
| − | |||
| − | |||
==Examples== | ==Examples== | ||
| Line 21: | Line 19: | ||
#SUPERLOGARITHM(190,32) = 1.1196675373624405 | #SUPERLOGARITHM(190,32) = 1.1196675373624405 | ||
#SUPERLOGARITHM(-76,4) = -2 | #SUPERLOGARITHM(-76,4) = -2 | ||
| + | |||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=Z5myJ8dg_rM&t=8s|280|center|Log}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 13:39, 4 February 2019
SUPERLOGARITHM (Number,Base)
SLOG (Number,Base)
- is any real number.
- is any positive real number.
Description
- This function shows the super logarithm of the given number.
- In , is the value to find log value.
- is the base value of the Log.
- Super-logarithm is one of the two inverse functions of tetration.
- This is also called Tetra logarithm.
- The two exponentiation function powers and exponentials have two inverse functions roots and logarithms,the two tetration functions tetra powers and tetra exponentials have two inverse functions tetra roots and tetra logarithms also called super roots and super logarithms.
- The super-logarithm, written is defined implicitly by
and
Examples
- SUPERLOGARITHM(23,6) = 1.3123124142065792
- SUPERLOGARITHM(190,32) = 1.1196675373624405
- SUPERLOGARITHM(-76,4) = -2
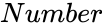 is any real number.
is any real number.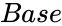 is any positive real number.
is any positive real number.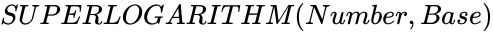 ,
,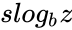 is defined implicitly by
is defined implicitly by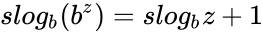 and
and