Difference between revisions of "Manuals/calci/PARTP"
Jump to navigation
Jump to search
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | =PARTP (n,k) | + | <div style="font-size:30px">'''PARTP (n,k)'''</div><br/> |
where | where | ||
*<math>n</math> and <math>k</math>are any integers. | *<math>n</math> and <math>k</math>are any integers. | ||
| − | + | **PARTP() shows the number of partitions of a given number. | |
| − | PARTP() shows the number of partitions of a given number. | ||
| Line 21: | Line 20: | ||
# PARTP(10,3) = 8 | # PARTP(10,3) = 8 | ||
# PARTP(54,10) = 29292 | # PARTP(54,10) = 29292 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=XN3Vy2M5ov8|280|center|Partitions}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 12:58, 11 March 2019
PARTP (n,k)
where
- and are any integers.
- PARTP() shows the number of partitions of a given number.
Description
PARTP(n,k)
- is any integer. is the number of ways.
- A partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers.
- Two sums that differ only in the order of their summands are considered the same partition.
- By convention, partitions are usually ordered from largest to smallest.
- Partition of a number is also called the number of unrestricted partition.
- When explicitly listing the partitions of a number n, the simplest form is the so-called natural representation which simply gives the sequence of numbers in the representation.
- The multiplicity representation instead gives the number of times each number occurs together with that number.
Examples
- PARTP(10,3) = 8
- PARTP(54,10) = 29292
Related Videos
See Also
References
 and
and 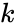 are any integers.
are any integers.