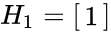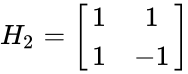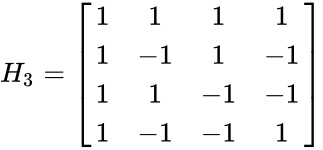Difference between revisions of "Manuals/calci/HADAMARD"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''HADAMARD'''</div><br/>") |
|||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size: | + | <div style="font-size:25px">'''MATRIX (TypeOfMatrix,DimensionsOfMatrix,SeedValuesToUse,IJFunction,PreParameter,IsItInternalCall)'''</div><br/> |
| + | *<math>TypeOfMatrix</math> is the type of the matrix. | ||
| + | *<math> DimensionsOfMatrix </math> is the order of the Hadamard matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the matrix satisfying the property of Hadamard. | ||
| + | *A Hadamard matrix is the square matrix with the entries of 1 and -1. | ||
| + | *Also the rows of that matrix are orthogonal. | ||
| + | *So H be a Hadamard matrix of order 2n. | ||
| + | *The transpose of H is closely related to its inverse. | ||
| + | *The equivalent definition for hadamard matrix is: | ||
| + | <math>H H^{T} = n I_{n}</math> | ||
| + | where <math>I_{n}</math> is the n × n identity matrix and <math>H^T</math> is the transpose of H. | ||
| + | *So the possible order of the matrix is 1,2 or positive multiple of 4. | ||
| + | *The few examples of hadamard matrices are: | ||
| + | *<math>H_1=\begin{bmatrix} | ||
| + | 1 \\ | ||
| + | \end{bmatrix}</math> | ||
| + | *<math>H_2 = \begin{bmatrix} | ||
| + | 1 & 1 \\ | ||
| + | 1 & -1 \\ | ||
| + | \end{bmatrix}</math> | ||
| + | *<math>H_3 =\begin{bmatrix} | ||
| + | 1 & 1 & 1 & 1 \\ | ||
| + | 1 & -1 & 1 & -1\\ | ||
| + | 1 & 1 & -1 & -1 \\ | ||
| + | 1 & -1 & -1 & 1\\ | ||
| + | \end{bmatrix}</math> | ||
| + | |||
| + | ==Examples== | ||
| + | *1.MATRIX("hadamard") = 1 | ||
| + | *2.MATRIX("hadamard",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || -1 || 1 || -1 | ||
| + | |- | ||
| + | | 1 || 1 || -1 || -1 | ||
| + | |- | ||
| + | |1 || -1 ||-1 || 1 | ||
| + | |} | ||
| + | *3.MATRIX("hadamard",4) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 1 || 1 || 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || -1 || 1 || -1 ||1 ||-1 ||1 ||-1 | ||
| + | |- | ||
| + | | 1 || 1 || -1 || -1 || 1 || 1 || -1 ||-1 | ||
| + | |- | ||
| + | |1 || -1 ||-1 || 1 || 1 || -1 || -1 || 1 | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 1 || -1 ||-1 ||-1 ||-1 | ||
| + | |- | ||
| + | | 1 || -1 || 1 ||-1 ||-1 || 1 || -1 ||1 | ||
| + | |- | ||
| + | | 1 || 1 || -1 || -1 || -1 || -1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || -1 || -1 || 1 || -1 ||1 || 1 ||-1 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=BM6TUF5dp9c|280|center|Hadamard Matrix}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/CIRCULANT| CIRCULANT]] | ||
| + | *[[Manuals/calci/HANKEL| HANKEL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Hadamard_matrix Hadamard matrix] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 12:46, 9 April 2019
MATRIX (TypeOfMatrix,DimensionsOfMatrix,SeedValuesToUse,IJFunction,PreParameter,IsItInternalCall)
- is the type of the matrix.
- is the order of the Hadamard matrix.
Description
- This function gives the matrix satisfying the property of Hadamard.
- A Hadamard matrix is the square matrix with the entries of 1 and -1.
- Also the rows of that matrix are orthogonal.
- So H be a Hadamard matrix of order 2n.
- The transpose of H is closely related to its inverse.
- The equivalent definition for hadamard matrix is:
where is the n × n identity matrix and is the transpose of H.
- So the possible order of the matrix is 1,2 or positive multiple of 4.
- The few examples of hadamard matrices are:
Examples
- 1.MATRIX("hadamard") = 1
- 2.MATRIX("hadamard",3)
| 1 | 1 | 1 | 1 |
| 1 | -1 | 1 | -1 |
| 1 | 1 | -1 | -1 |
| 1 | -1 | -1 | 1 |
- 3.MATRIX("hadamard",4)
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 |
| 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 |
| 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 |
| 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 |
| 1 | -1 | 1 | -1 | -1 | 1 | -1 | 1 |
| 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 |
| 1 | -1 | -1 | 1 | -1 | 1 | 1 | -1 |
Related Videos
See Also
References
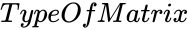 is the type of the matrix.
is the type of the matrix.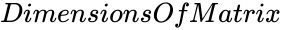 is the order of the Hadamard matrix.
is the order of the Hadamard matrix.
 is the n × n identity matrix and
is the n × n identity matrix and 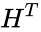 is the transpose of H.
is the transpose of H.