Difference between revisions of "Manuals/calci/ANTIDIAGONAL"
Jump to navigation
Jump to search
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size: | + | <div style="font-size:25px">'''MATRIX (TypeOfMatrix,DimensionsOfMatrix,SeedValuesToUse,IJFunction,PreParameter,IsItInternalCall)'''</div><br/> |
| − | *<math> | + | *<math>TypeOfMatrix</math> is the type of the matrix. |
| + | *<math> DimensionsOfMatrix </math> is the order of the Anti diagonal matrix. | ||
==Description== | ==Description== | ||
| Line 10: | Line 11: | ||
*2. If A and D are n×n anti-diagonal and diagonal matrices, respectively, then AD,DA are anti-diagonal. | *2. If A and D are n×n anti-diagonal and diagonal matrices, respectively, then AD,DA are anti-diagonal. | ||
*3.All anti-diagonal matrices are also persymmetric. | *3.All anti-diagonal matrices are also persymmetric. | ||
| − | |||
*To display the different order of matrices then the syntax is MATRIX("anti-diagonal",5). | *To display the different order of matrices then the syntax is MATRIX("anti-diagonal",5). | ||
==Examples== | ==Examples== | ||
| − | *MATRIX("ANTI-DIAGONAL") | + | *MATRIX("ANTI-DIAGONAL") = 1 |
| + | *MATRIX("ANTI-DIAGONAL",3) | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 47: | Line 48: | ||
*[[Manuals/calci/ARROWHEAD| ARROWHEAD]] | *[[Manuals/calci/ARROWHEAD| ARROWHEAD]] | ||
*[[Manuals/calci/MATRIXOPERATORS| MATRIXOPERATORS]] | *[[Manuals/calci/MATRIXOPERATORS| MATRIXOPERATORS]] | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=wbVMXohzcQU|280|center|Diagonal Matrix}} | ||
==References== | ==References== | ||
*[http://en.wikipedia.org/wiki/Anti-diagonal_matrix Anti Diagonal] | *[http://en.wikipedia.org/wiki/Anti-diagonal_matrix Anti Diagonal] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 13:30, 9 April 2019
MATRIX (TypeOfMatrix,DimensionsOfMatrix,SeedValuesToUse,IJFunction,PreParameter,IsItInternalCall)
- is the type of the matrix.
- is the order of the Anti diagonal matrix.
Description
- This function gives the matrix satisfying the anti diagonal properties.
- An anti-diagonal matrix is a matrix where all the entries are zero except those on the diagonal going from the lower left corner to the upper right corner (), known as the anti-diagonal.
- So here we are getting all entries are 0 except from the opposite of main diagonal as 1.
- The properties of anti diagonal matrix are:
- 1.The product of two anti-diagonal matrices is a diagonal matrix.
- 2. If A and D are n×n anti-diagonal and diagonal matrices, respectively, then AD,DA are anti-diagonal.
- 3.All anti-diagonal matrices are also persymmetric.
- To display the different order of matrices then the syntax is MATRIX("anti-diagonal",5).
Examples
- MATRIX("ANTI-DIAGONAL") = 1
- MATRIX("ANTI-DIAGONAL",3)
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
- MATRIX("anti-diagonal",4,200..204)
| 0 | 0 | 0 | 200 |
| 0 | 0 | 201 | 0 |
| 0 | 202 | 0 | 0 |
| 203 | 0 | 0 | 0 |
- MATRIX("anti-diagonal",3,-32.05)
| 0 | 0 | -32.05 |
| 0 | -32.05 | 0 |
| -32.05 | 0 | 0 |
See Also
Related Videos
References
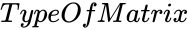 is the type of the matrix.
is the type of the matrix.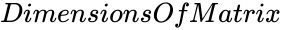 is the order of the Anti diagonal matrix.
is the order of the Anti diagonal matrix. ), known as the anti-diagonal.
), known as the anti-diagonal.