Difference between revisions of "Manuals/calci/SVF"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''SVF (Matrix)'''</div><br/> *<math>Matrix</math> is any set of values. ==Description== *This function shows the Singular value of a given matri...") |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
*To find Singular Value Decomposition we have to follow the below rules: | *To find Singular Value Decomposition we have to follow the below rules: | ||
*The left-singular vectors of the matrix M are a set of orthonormal eigenvectors of MM∗. | *The left-singular vectors of the matrix M are a set of orthonormal eigenvectors of MM∗. | ||
| − | *The right-singular vectors of M are a set of orthonormal eigenvectors of <math>M^ | + | *The right-singular vectors of M are a set of orthonormal eigenvectors of <math>M^*M</math>. |
| − | *The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of both <math>M^ | + | *The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of both <math>M^*M</math> and <math>MM^*</math>. |
| + | |||
| + | ==Examples== | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=4g-zS32oKEw|280|center|Singular Values}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/LUDECOMPOSITION | LUDECOMPOSITION ]] | ||
| + | *[[Manuals/calci/CHOLESKYFACTORIZATION | CHOLESKYFACTORIZATION ]] | ||
| + | *[[Manuals/calci/QRDECOMPOSITION | QRDECOMPOSITION ]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Singular_value_decomposition Decomposition] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 12:05, 25 April 2019
SVF (Matrix)
- is any set of values.
Description
- This function shows the Singular value of a given matrix in descending order.
- In , is any matrix with array of values.
- Singular value decomposition is defined by the factorization of a real or complex matrix.
- It is the generalization of the Eigen decomposition of a symmetric matrix with positive eigen values to any mxn matrix through an extension of the polar decomposition.
- Singular value decomposition is of the form where is any square real or complex Unitary matrix of order .
- is a mxn rectangular diagonal matrix with non negative real numbers.
- V is also any square real or complex Unitary matrix of order nxn.
- The columns of U and V are called left Singular and right Singular vectors of the matrix.
- To find Singular Value Decomposition we have to follow the below rules:
*The left-singular vectors of the matrix M are a set of orthonormal eigenvectors of MM∗. *The right-singular vectors of M are a set of orthonormal eigenvectors of . *The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of both and .
Examples
Related Videos
See Also
References
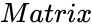 is any set of values.
is any set of values.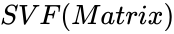 ,
, 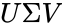 where
where 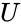 is any square real or complex Unitary matrix of order
is any square real or complex Unitary matrix of order 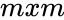 .
.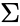 is a mxn rectangular diagonal matrix with non negative real numbers.
is a mxn rectangular diagonal matrix with non negative real numbers.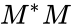 .
*The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of both
.
*The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of both 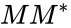 .
.