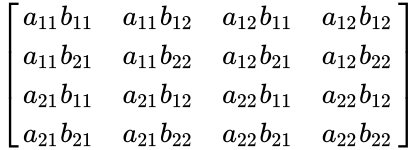Difference between revisions of "Manuals/calci/MATRIXTENSORPRODUCT"
Jump to navigation
Jump to search
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size: | + | <div style="font-size:25px">'''MATRIXTENSORPRODUCT (a,b) '''</div><br/> |
*<math>a</math> and <math>b</math> are any two matrices. | *<math>a</math> and <math>b</math> are any two matrices. | ||
| Line 10: | Line 10: | ||
*The Tensor product is defined by the product two vector spaces V and W is itself a Vector space. | *The Tensor product is defined by the product two vector spaces V and W is itself a Vector space. | ||
*It is denoted by <math>V\otimes W</math>. | *It is denoted by <math>V\otimes W</math>. | ||
| + | *A [http://wiki.zcubes.com/Manuals/calci/DYADIC DYADIC] product is the special case of the tensor product between two vectors of the same dimension. | ||
*The tensor product of V and W is the vector space generated by the symbols <math>v\otimes w </math>, with <math>v \isin V</math> and <math>w \isin W</math>. | *The tensor product of V and W is the vector space generated by the symbols <math>v\otimes w </math>, with <math>v \isin V</math> and <math>w \isin W</math>. | ||
*The tensor product from the direct sum vector space, whose dimension is the sum of the dimensions of the two summands: | *The tensor product from the direct sum vector space, whose dimension is the sum of the dimensions of the two summands: | ||
| Line 29: | Line 30: | ||
b_{21} & b_{22} | b_{21} & b_{22} | ||
\end{bmatrix} \\ | \end{bmatrix} \\ | ||
| − | + | ||
a_{21} \begin{bmatrix} | a_{21} \begin{bmatrix} | ||
b_{11} & b_{12} \\ | b_{11} & b_{12} \\ | ||
| Line 45: | Line 46: | ||
a_{21}b_{21} & a_{21}b_{22} & a_{22}b_{21} & a_{22}b_{22} | a_{21}b_{21} & a_{21}b_{22} & a_{22}b_{21} & a_{22}b_{22} | ||
\end{bmatrix} </math> | \end{bmatrix} </math> | ||
| + | |||
| + | ==Examples== | ||
| + | 1. MATRIXTENSORPRODUCT([[2,6],[-4,9]],[[8,5],[3,12]]) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |16 ||10 ||48 ||30 | ||
| + | |- | ||
| + | |6 ||24 ||18|| 72 | ||
| + | |- | ||
| + | | -32|| -20 || 72||45 | ||
| + | |- | ||
| + | | -12 || -48 || 27 ||108 | ||
| + | |} | ||
| + | 2. MATRIXTENSORPRODUCT([[3,7.3,6],[10,11,-6],[8,5,3]],[[12,4,-5],[6,10,3],[3.5,9,5.4]]) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |36 || 12|| -15 ||87.6 ||29.2||-36.5||72||24||-30 | ||
| + | |- | ||
| + | |18 || 30 ||9 ||43.8|| 73||21.9||36|| 60|| 18 | ||
| + | |- | ||
| + | |10.5 ||27||16.200000000000003||25.55|| 65.7||39.42||21||54||32.400000000000006 | ||
| + | |- | ||
| + | |120 || 40||-50||132||44||-55|| -72||-24||30 | ||
| + | |- | ||
| + | |60 || 100||30 ||66 || 110 || 33 || -36 ||-60 ||-18 | ||
| + | |- | ||
| + | |35 || 90 || 54 ||38.5||99 ||59.400000000000006 || -21||-54||-32.400000000000006 | ||
| + | |- | ||
| + | |96 || 32 || -40 || 60 || 20 || -25 || 36 || 12 ||-15 | ||
| + | |- | ||
| + | |48 || 80 ||24 || 30 || 50 || 15 || 18 || 30 ||9 | ||
| + | |- | ||
| + | |28 || 72 || 43.2 || 17.5 || 45 ||27 ||10.5 || 27||16.200000000000003 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=tpL95Sd7zT0&t=81s|280|center|Tensor Product}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/CHOLESKYFACTORIZATION| CHOLESKYFACTORIZATION]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/PASCAL| PASCAL]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Tensor_product Tensor Product] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 12:33, 29 April 2019
MATRIXTENSORPRODUCT (a,b)
- and are any two matrices.
Description
- This function shows the Tensor product of the matrix.
- In , and are any two matrices.
- Here matrices and should be square matrix with same order.
- Tensor product is denoted by .
- Tensor product is different from general product.
- The Tensor product is defined by the product two vector spaces V and W is itself a Vector space.
- It is denoted by .
- A DYADIC product is the special case of the tensor product between two vectors of the same dimension.
- The tensor product of V and W is the vector space generated by the symbols , with and .
- The tensor product from the direct sum vector space, whose dimension is the sum of the dimensions of the two summands:
- Now consider any 2x2 matrices:
=
Examples
1. MATRIXTENSORPRODUCT([[2,6],[-4,9]],[[8,5],[3,12]])
| 16 | 10 | 48 | 30 |
| 6 | 24 | 18 | 72 |
| -32 | -20 | 72 | 45 |
| -12 | -48 | 27 | 108 |
2. MATRIXTENSORPRODUCT([[3,7.3,6],[10,11,-6],[8,5,3]],[[12,4,-5],[6,10,3],[3.5,9,5.4]])
| 36 | 12 | -15 | 87.6 | 29.2 | -36.5 | 72 | 24 | -30 |
| 18 | 30 | 9 | 43.8 | 73 | 21.9 | 36 | 60 | 18 |
| 10.5 | 27 | 16.200000000000003 | 25.55 | 65.7 | 39.42 | 21 | 54 | 32.400000000000006 |
| 120 | 40 | -50 | 132 | 44 | -55 | -72 | -24 | 30 |
| 60 | 100 | 30 | 66 | 110 | 33 | -36 | -60 | -18 |
| 35 | 90 | 54 | 38.5 | 99 | 59.400000000000006 | -21 | -54 | -32.400000000000006 |
| 96 | 32 | -40 | 60 | 20 | -25 | 36 | 12 | -15 |
| 48 | 80 | 24 | 30 | 50 | 15 | 18 | 30 | 9 |
| 28 | 72 | 43.2 | 17.5 | 45 | 27 | 10.5 | 27 | 16.200000000000003 |
 and
and 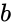 are any two matrices.
are any two matrices.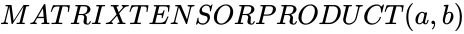 ,
,  .
.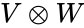 .
.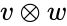 , with
, with 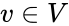 and
and 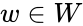 .
.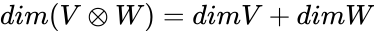
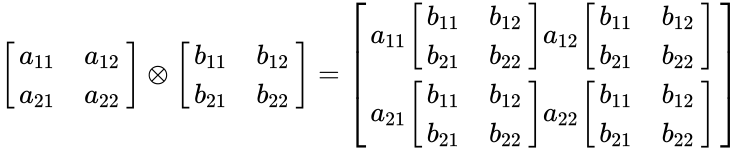 =
=