Difference between revisions of "Manuals/calci/SVD"
Jump to navigation
Jump to search
| (17 intermediate revisions by 2 users not shown) | |||
| Line 6: | Line 6: | ||
*Where the columns of U and V are orthonormal and the matrix S is diagonal with positive real entries | *Where the columns of U and V are orthonormal and the matrix S is diagonal with positive real entries | ||
*Singular value decomposition is defined for all matrices (rectangular or square). | *Singular value decomposition is defined for all matrices (rectangular or square). | ||
| + | *The rank of a matrix is equal to the number of non-zero singular values. | ||
| + | |||
Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers. | Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers. | ||
| Line 15: | Line 17: | ||
V is an n × n unitary matrix over K, and | V is an n × n unitary matrix over K, and | ||
<math>V^T</math> is the conjugate transpose of V. | <math>V^T</math> is the conjugate transpose of V. | ||
| + | |||
| + | ==Example== | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !!C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 1 || 0 || 1 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | -1 || -2 || 0 | ||
| + | |- | ||
| + | ! 3 | ||
| + | |0 || 1 || -1 | ||
| + | |} | ||
| + | =SVD(A1:C3) | ||
| + | {| border="1" cellpadding="5" cellspacing="0" | ||
| + | |- | ||
| + | | | ||
| + | 0.12000026038175768 -0.8097122815927454 -0.5744266346072238 | ||
| + | || | ||
| + | -0.9017526469088556 0.15312282248412068 -0.40422217285469236 | ||
| + | || | ||
| + | 0.41526148545366265 0.5664975042066532 -0.7117854145923829 | ||
| + | |- | ||
| + | | | ||
| + | 2.4605048700187635 0 0 | ||
| + | || | ||
| + | 0 1.699628148275319 0 | ||
| + | || | ||
| + | 0 0 0.23912327825655444 | ||
| + | |- | ||
| + | | | ||
| + | 0.4152614854539272 -0.566497504206459 -0.711854145923831 | ||
| + | || | ||
| + | 0.9017526469087841 0.15312282248454143 0.4042221728546923 | ||
| + | || | ||
| + | -0.12000026038137995 -0.8097122815928015 0.5744266346072238 | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !!C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 1 || 2 || 3 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 4 || 5 || 6 | ||
| + | |- | ||
| + | ! 3 | ||
| + | | 7|| 8 || 9 | ||
| + | |} | ||
| + | =SVD(A1:C3) | ||
| + | {| border="1" cellpadding="5" cellspacing="0" | ||
| + | |- | ||
| + | | | ||
| + | 0.21483723836830051 0.8872306883463938 0.4082482904638627 | ||
| + | || | ||
| + | 0.5205873894647103 0.2496439529883539 -0.8164965809277261 | ||
| + | || | ||
| + | 0.82633754056112 -0.3879427823696853 0.4082482904638632 | ||
| + | |- | ||
| + | | | ||
| + | 16.848103352614217 0 0 | ||
| + | || | ||
| + | 0 1.0683695145547085 0 | ||
| + | || | ||
| + | 0 0 0 | ||
| + | |- | ||
| + | | | ||
| + | 0.4796711778777768 -0.7766909903215562 0.40824829046386296 | ||
| + | || | ||
| + | 0.5723677939720628 -0.0756864701045544 -0.816496580927726 | ||
| + | || | ||
| + | 0.6650644100663488 0.6253180501124471 0.40824829046386313 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=Ls2TgGFfZnU|280|center|Singular Value Decomposition}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/LUDECOMPOSITION | LUDECOMPOSITION ]] | ||
| + | *[[Manuals/calci/CHOLESKYFACTORIZATION | CHOLESKYFACTORIZATION ]] | ||
| + | *[[Manuals/calci/QRDECOMPOSITION | QRDECOMPOSITION ]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Singular_value_decomposition Decomposition] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 13:34, 2 May 2019
SVD(Matrix)
- is the set of values.
Description
- The singular value decomposition of a matrix A is the factorization of A into the product of three matrices
- Where the columns of U and V are orthonormal and the matrix S is diagonal with positive real entries
- Singular value decomposition is defined for all matrices (rectangular or square).
- The rank of a matrix is equal to the number of non-zero singular values.
Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers.
- Then there exists a factorization, called a singular value decomposition of A, of the form
where U is an m × m unitary matrix, S is a diagonal m × n matrix with non-negative real numbers on the diagonal, V is an n × n unitary matrix over K, and is the conjugate transpose of V.
Example
| A | B | C | |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | -1 | -2 | 0 |
| 3 | 0 | 1 | -1 |
=SVD(A1:C3)
0.12000026038175768 -0.8097122815927454 -0.5744266346072238 |
-0.9017526469088556 0.15312282248412068 -0.40422217285469236 |
0.41526148545366265 0.5664975042066532 -0.7117854145923829 |
2.4605048700187635 0 0 |
0 1.699628148275319 0 |
0 0 0.23912327825655444 |
0.4152614854539272 -0.566497504206459 -0.711854145923831 |
0.9017526469087841 0.15312282248454143 0.4042221728546923 |
-0.12000026038137995 -0.8097122815928015 0.5744266346072238 |
| A | B | C | |
|---|---|---|---|
| 1 | 1 | 2 | 3 |
| 2 | 4 | 5 | 6 |
| 3 | 7 | 8 | 9 |
=SVD(A1:C3)
0.21483723836830051 0.8872306883463938 0.4082482904638627 |
0.5205873894647103 0.2496439529883539 -0.8164965809277261 |
0.82633754056112 -0.3879427823696853 0.4082482904638632 |
16.848103352614217 0 0 |
0 1.0683695145547085 0 |
0 0 0 |
0.4796711778777768 -0.7766909903215562 0.40824829046386296 |
0.5723677939720628 -0.0756864701045544 -0.816496580927726 |
0.6650644100663488 0.6253180501124471 0.40824829046386313 |
Related Videos
See Also
References
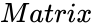 is the set of values.
is the set of values.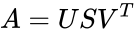
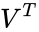 is the conjugate transpose of V.
is the conjugate transpose of V.