Difference between revisions of "Manuals/calci/ANTILOG"
Jump to navigation
Jump to search
| (3 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
#ANTILOG(3.23621726987935,3) = 35.000000000000014 = 35(Approximate) | #ANTILOG(3.23621726987935,3) = 35.000000000000014 = 35(Approximate) | ||
#ANTILOG(2.397940008672037,10) = 249.9999999999997 = 250 (Approximate) | #ANTILOG(2.397940008672037,10) = 249.9999999999997 = 250 (Approximate) | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=vZ709qOc8x8|280|center|Inverse Log}} | ||
==See Also== | ==See Also== | ||
| Line 20: | Line 24: | ||
*[[Manuals/calci/LN| LN]] | *[[Manuals/calci/LN| LN]] | ||
| − | + | ==References== | |
| − | + | *[http://www.rapidtables.com/calc/math/anti-log-calculator.htm AntiLog] | |
*[[Z_API_Functions | List of Main Z Functions]] | *[[Z_API_Functions | List of Main Z Functions]] | ||
*[[ Z3 | Z3 home ]] | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 01:28, 1 July 2019
ANTILOG (Number,Base)
- is the log value to find the Antilog value
- base value of the Log value.
Description
- This function shows the antilog of a given number.
- Antilog is the number whose logarithm is a given number.
- For example, the logarithm of 1,000 (10 3) is 3, so the antilogarithm of 3 is 1,000.
- In algebraic notation, if log x = y, then antilog y = x.
- Here ANTILOG(Number, Base) indicates we can find the anti logarithmic value with any base.
Examples
- ANTILOG(3.3219280948873626,2) = 10.000000000000002 =10(Approximate)
- ANTILOG(3.23621726987935,3) = 35.000000000000014 = 35(Approximate)
- ANTILOG(2.397940008672037,10) = 249.9999999999997 = 250 (Approximate)
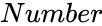 is the log value to find the Antilog value
is the log value to find the Antilog value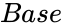 base value of the Log value.
base value of the Log value.