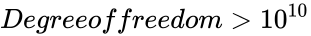Difference between revisions of "Manuals/calci/CHIDIST"
Jump to navigation
Jump to search
| (36 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''CHIDIST( | + | <div style="font-size:30px">'''CHIDIST (Number,DegreeOfFreedom)'''</div><br/> |
| − | * | + | *<math>Number</math> is the value for which distribution is evaluated. |
| + | *<math>Degreeoffreedom</math> is the number of degrees of freedom. | ||
| + | **CHIDIST(), returns the one-tailed probability of the chi-squared distribution. | ||
==Description== | ==Description== | ||
*This function gives the one_tailed probability of the chi-squared distribution. | *This function gives the one_tailed probability of the chi-squared distribution. | ||
| − | *It is denoted by | + | *It is denoted by <math>\chi^2</math> distribution. |
| − | *The | + | *Normally categorical data's may displayed in tables. |
| − | * | + | *The <math>\chi^2</math> static used to compare the observed value in each table to the assumed value. |
| + | *The conditions of <math>\chi^2</math> test is | ||
| + | #The table should be 2x2 or more than 2x2 | ||
| + | #Each observations should not be dependent | ||
| + | #All expected values should be 10 or greater. | ||
| + | *The test statistic is: | ||
| + | <math>\chi^2=\sum\frac{(Oi-Ei)^2}{Ei}</math> | ||
| + | The degrees of freedom is: (r–1)(c–1) | ||
| + | *r = No. of rows | ||
| + | *c = No. of columns | ||
| + | Where: | ||
| + | *Oi-the observed value in the ith cell | ||
| + | *Ei- the expected value in the ith cell | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Also this function will the result as Error when | Also this function will the result as Error when | ||
| − | + | #The <math>Number</math> & <math>Degreeoffreedom</math> values are non-numeric | |
| − | + | #The <math>Number</math> value is negative or <math>Degreeoffreedom</math> value is not an integer | |
| − | + | #The <math>Degreeoffreedom < 1</math> or <math>Degreeoffreedom > 10^{10}</math> | |
| − | + | #Here CHIDIST=P(X>x),where X is a <math>\chi^2</math> random variable. | |
| + | |||
| + | *CHIDIST(-2,1)=Error, because Number is negative. | ||
| + | *CHIDIST(2,-1)=Error, because Degreeoffreedom<1 | ||
| − | **<math> | + | ==ZOS== |
| − | * | + | *The syntax is to calculate CHIDIST in ZOS is CHIDIST(Number,Degreeoffreedom). |
| + | *<math>Number</math> is the value for which distribution is evaluated. | ||
| + | *<math>Degreeoffreedom</math> is the number of degrees of freedom. | ||
| + | *For e.g.,CHIDIST(10..12,5.1..7.1..0.6) | ||
| + | {{#ev:youtube|44cEta1FnA4|280|center|Chi-squared Distribution}} | ||
==Examples== | ==Examples== | ||
{| id="TABLE3" class="SpreadSheet blue" | {| id="TABLE3" class="SpreadSheet blue" | ||
|- class="even" | |- class="even" | ||
| − | | CHIDIST( | + | | CHIDIST(Number,Degreeoffreedom) |
! x | ! x | ||
! df | ! df | ||
| Line 53: | Line 64: | ||
|- class="even" | |- class="even" | ||
|CHIDIST(-2,1) | |CHIDIST(-2,1) | ||
| − | |2 | + | | -2 |
|1 | |1 | ||
| − | | | + | |#N/A (NUMBER > 0) |
|- class="odd" | |- class="odd" | ||
|CHIDIST(2,-1) | |CHIDIST(2,-1) | ||
|2 | |2 | ||
| − | |1 | + | | -1 |
| − | | | + | |null |
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|dXB3cUGnaxQ|280|center|Chi-Square Distribution}} | ||
==See Also== | ==See Also== | ||
| − | |||
*[[Manuals/calci/CHITEST | CHITEST]] | *[[Manuals/calci/CHITEST | CHITEST]] | ||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/ | + | [http://en.wikipedia.org/wiki/Chi-squared_distribution CHI-SQUARE Distribution] |
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 09:50, 2 June 2020
CHIDIST (Number,DegreeOfFreedom)
- is the value for which distribution is evaluated.
- is the number of degrees of freedom.
- CHIDIST(), returns the one-tailed probability of the chi-squared distribution.
Description
- This function gives the one_tailed probability of the chi-squared distribution.
- It is denoted by distribution.
- Normally categorical data's may displayed in tables.
- The static used to compare the observed value in each table to the assumed value.
- The conditions of test is
- The table should be 2x2 or more than 2x2
- Each observations should not be dependent
- All expected values should be 10 or greater.
- The test statistic is:
The degrees of freedom is: (r–1)(c–1)
- r = No. of rows
- c = No. of columns
Where:
- Oi-the observed value in the ith cell
- Ei- the expected value in the ith cell
Also this function will the result as Error when
- The & values are non-numeric
- The value is negative or value is not an integer
- The or
- Here CHIDIST=P(X>x),where X is a random variable.
- CHIDIST(-2,1)=Error, because Number is negative.
- CHIDIST(2,-1)=Error, because Degreeoffreedom<1
ZOS
- The syntax is to calculate CHIDIST in ZOS is CHIDIST(Number,Degreeoffreedom).
- is the value for which distribution is evaluated.
- is the number of degrees of freedom.
- For e.g.,CHIDIST(10..12,5.1..7.1..0.6)
Examples
| CHIDIST(Number,Degreeoffreedom) | x | df | RESULT |
|---|---|---|---|
| CHIDIST(18,2) | 18 | 2 | 0.0001234098 |
| CHIDIST(15,1) | 15 | 1 | 0.0001075112 |
| CHIDIST(2,1) | 2 | 1 | 0.157299207050 |
| CHIDIST(-2,1) | -2 | 1 | #N/A (NUMBER > 0) |
| CHIDIST(2,-1) | 2 | -1 | null |
Related Videos
See Also
References
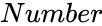 is the value for which distribution is evaluated.
is the value for which distribution is evaluated.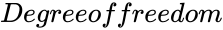 is the number of degrees of freedom.
is the number of degrees of freedom.
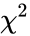 distribution.
distribution.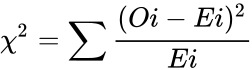 The degrees of freedom is: (r–1)(c–1)
The degrees of freedom is: (r–1)(c–1)
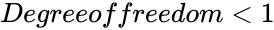 or
or