Difference between revisions of "POLAR"

From ZCubes Wiki
Jump to navigation Jump to search
(Created page with "<div style="font-size:30px">'''RADAR CHART'''</div> ==='''''Description:'''''=== '''''The Radar Chart, also sometimes called a spider or star chart, lets us compare multiple i...")
 
 
(9 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
<div style="font-size:30px">'''RADAR CHART'''</div>
+
<div style="font-size:30px">'''POLAR CHART'''</div>
 
==='''''Description:'''''===
 
==='''''Description:'''''===
−
'''''The Radar Chart, also sometimes called a spider or star chart, lets us compare multiple items against multiple criteria.'''''<br>
+
'''''In Polar Charts, a series is represented by a closed curve that connects points in the polar coordinate system.'''''<br>
−
'''''You could use it to see how temperatures change in multiple locations over the course of a year, or quickly compare products in several different areas.''''' <br>
+
'''''Each data point is determined by the distance from the pole (the radial coordinate) and the angle from the fixed direction (the angular coordinate).'''''<br>
−
*'''''Radar Chart has X & Y axis.  
+
*'''''Graphing a point with polar coordinates (r, θ).'''''<br>
−
*'''''The x-axis is nothing but each end of the spider and each step of the spider considered as Y-axis.
+
*'''''In polar coordinates, the dependent variable, r, gives not a height but a distance from the pole in direction θ.'''''<br>
−
*'''''Zero point of the radar chart starts from the centre of the wheel. Towards the edge of the spike, a point reaches, the higher the value.
+
*''''' When graphing an equation in polar coordinates, we think of sweeping around the pole in the counterclockwise direction, and at each angle θ, the r-value tells us how far the graph is from the pole.'''''<br>
−
*'''''It is a X vs (Y1,[Y2]....) graph.'''''
 
−
**'''''X-axis represents one set of data.
 
−
**'''''Y-axis can represent single or multiple data sets.
 
  
 
==Example==
 
==Example==
Line 15: Line 12:
 
| A|| '''B''' || '''C'''
 
| A|| '''B''' || '''C'''
 
|-
 
|-
−
| Theta || '''deg Theta''' || '''rad'''  
+
| Theta || '''deg Theta''' || '''rad (SIN(θ))'''  
 
|-
 
|-
−
| 0 || 0 || 0   
+
| 0 || 0° || 0   
 
|-
 
|-
−
| 0.3307 || 18.9477 || 0.3247
+
| 0.3307 || 18.9477° || 0.3247
 
|-
 
|-
−
| 0.6614 || 37.8954 || 0.6142
+
| 0.6614 || 37.8954° || 0.6142
 
|-
 
|-
−
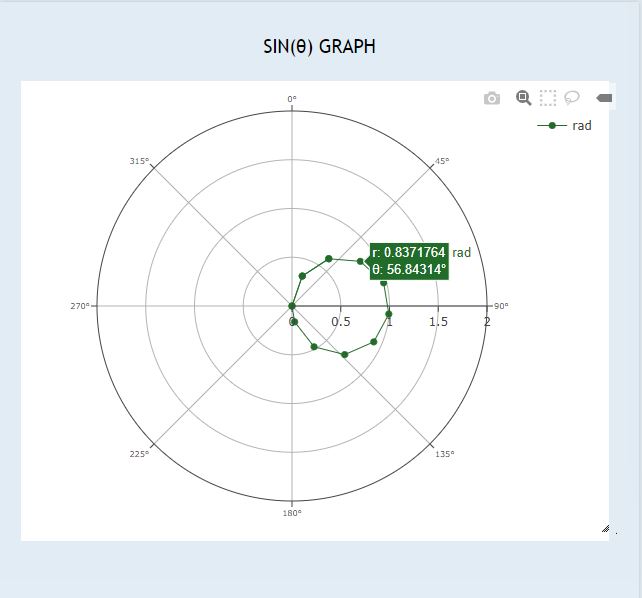
| 0.9921 || 56.8431 || 0.8372
+
| 0.9921 || 56.8431° || 0.8372
 
|-
 
|-
−
| 1.3228 || 75.7909 || 0.9694
+
| 1.3228 || 75.7909° || 0.9694
 
|-
 
|-
−
|1.6535 || 94.7386 || 0.9966
+
|1.6535 || 94.7386° || 0.9966
 
|-
 
|-
−
|1.9842 || 113.6863 || 0.9158
+
|1.9842 || 113.6863° || 0.9158
 
|-
 
|-
−
|2.3149 || 132.6340 || 0.7357
+
|2.3149 || 132.6340° || 0.7357
 
|-
 
|-
−
|2.6456 || 151.5817 || 0.4749
+
|2.6456 || 151.5817° || 0.4749
 
|-
 
|-
−
|2.9763 || 170.5294 || 0.1645
+
|2.9763 || 170.5294° || 0.1645
 
|-
 
|-
−
|3.3070 || 189.4771 || -0.16
+
|3.3070 || 189.4771° || -0.16
 
|-
 
|-
−
|3.6377 || 208.4249 || -0.48
+
|3.6377 || 208.4249° || -0.48
 
|-
 
|-
−
|3.9684 || 227.3726 || -0.74
+
|3.9684 || 227.3726° || -0.74
 
|-
 
|-
−
|4.2991 || 246.3203 || -0.92  
+
|4.2991 || 246.3203° || -0.92  
 
|-
 
|-
−
|4.6298 || 265.2680 || -1.00
+
|4.6298 || 265.2680° || -1.00
 
|-
 
|-
−
|4.9605 || 284.2157 || -0.97  
+
|4.9605 || 284.2157° || -0.97  
 
|-
 
|-
−
|5.2912 || 303.1634 || -0.84  
+
|5.2912 || 303.1634° || -0.84  
 
|-
 
|-
−
|5.6219 || 322.1111 || -0.61
+
|5.6219 || 322.1111° || -0.61
 
|-
 
|-
−
|5.9526 || 341.0589 || -0.32
+
|5.9526 || 341.0589° || -0.32
 
|-
 
|-
−
|6.2833 || 360.0066 || 0.0001
+
|6.2833 || 360.0066° || 0.0001
 
|-
 
|-
−
|6.6140 || 378.9543 || 0.3248
+
|6.6140 || 378.9543° || 0.3248
 
|-
 
|-
−
|6.9447 || 397.9020 || 0.6143
+
|6.9447 || 397.9020° || 0.6143
 
|}
 
|}
  

Latest revision as of 10:07, 10 June 2020

POLAR CHART

Description:

In Polar Charts, a series is represented by a closed curve that connects points in the polar coordinate system.
Each data point is determined by the distance from the pole (the radial coordinate) and the angle from the fixed direction (the angular coordinate).

  • Graphing a point with polar coordinates (r, θ).
  • In polar coordinates, the dependent variable, r, gives not a height but a distance from the pole in direction θ.
  • When graphing an equation in polar coordinates, we think of sweeping around the pole in the counterclockwise direction, and at each angle θ, the r-value tells us how far the graph is from the pole.

Example

A B C
Theta deg Theta rad (SIN(θ))
0 0° 0
0.3307 18.9477° 0.3247
0.6614 37.8954° 0.6142
0.9921 56.8431° 0.8372
1.3228 75.7909° 0.9694
1.6535 94.7386° 0.9966
1.9842 113.6863° 0.9158
2.3149 132.6340° 0.7357
2.6456 151.5817° 0.4749
2.9763 170.5294° 0.1645
3.3070 189.4771° -0.16
3.6377 208.4249° -0.48
3.9684 227.3726° -0.74
4.2991 246.3203° -0.92
4.6298 265.2680° -1.00
4.9605 284.2157° -0.97
5.2912 303.1634° -0.84
5.6219 322.1111° -0.61
5.9526 341.0589° -0.32
6.2833 360.0066° 0.0001
6.6140 378.9543° 0.3248
6.9447 397.9020° 0.6143

POLARCHART(A1:C23)

Polar.JPG

GRAPHING MAIN PAGE

Retrieved from "http://wiki.zcubes.com/index.php?title=POLAR&oldid=214124"