Difference between revisions of "HELIANTHUS ANNUUS"
Jump to navigation
Jump to search
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''HELIANTHUS ANNUUS'''</div> | <div style="font-size:30px">'''HELIANTHUS ANNUUS'''</div> | ||
| − | ===''' | + | ==='''DESCRIPTION'''=== |
| − | + | '''In Polar Charts, a series is represented by a closed curve that connects points in the polar coordinate system.'''<br> | |
| − | + | '''Each data point is determined by the distance from the pole (the radial coordinate) and the angle from the fixed direction (the angular coordinate).'''<br> | |
*'''''Graphing a point with polar coordinates (r, θ).'''''<br> | *'''''Graphing a point with polar coordinates (r, θ).'''''<br> | ||
*'''''In polar coordinates, the dependent variable, r, gives not a height but a distance from the pole in direction θ.'''''<br> | *'''''In polar coordinates, the dependent variable, r, gives not a height but a distance from the pole in direction θ.'''''<br> | ||
*''''' When graphing an equation in polar coordinates, we think of sweeping around the pole in the counterclockwise direction, and at each angle θ, the r-value tells us how far the graph is from the pole.'''''<br><br/> | *''''' When graphing an equation in polar coordinates, we think of sweeping around the pole in the counterclockwise direction, and at each angle θ, the r-value tells us how far the graph is from the pole.'''''<br><br/> | ||
| − | ==='''MODEL | + | ==='''MODEL'''=== |
| − | '''A model for the pattern of florets in the head of a sunflower was proposed by H. Vogel in 1979.'''<br | + | '''A model for the pattern of florets in the head of a sunflower was proposed by H. Vogel in 1979.'''<br> |
'''This is expressed in polar coordinates:'''<br> | '''This is expressed in polar coordinates:'''<br> | ||
:<math>r=c \sqrt{n},</math> | :<math>r=c \sqrt{n},</math> | ||
| Line 16: | Line 16: | ||
'''''n is the index number of the floret'''''<br> | '''''n is the index number of the floret'''''<br> | ||
''''' c is a constant scaling factor'''''<br><br/> | ''''' c is a constant scaling factor'''''<br><br/> | ||
| − | '''It is a form of Fermat's spiral. The angle 137.5° is related to the golden ratio (55/144 of a circular angle, where 55 and 144 are Fibonacci numbers) and gives a close packing of florets.'''<br> | + | *'''It is a form of Fermat's spiral.<br> |
| + | *'''The angle 137.5° is related to the golden ratio (55/144 of a circular angle, where 55 and 144 are Fibonacci numbers) and gives a close packing of florets.'''<br><br/> | ||
| − | ==='''EXPRESSION | + | ==='''EXPRESSION'''=== |
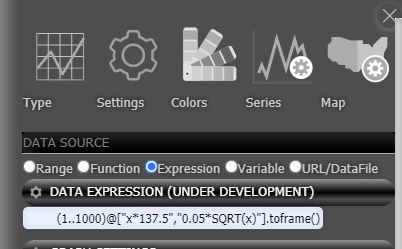
'''Expression used in plotting:'''<br> | '''Expression used in plotting:'''<br> | ||
| + | '''Plotting from n = 1 to 1000,<br> | ||
'''(1..1000)@["x*137.5","0.05*SQRT(x)"].toframe()'''<br><br/> | '''(1..1000)@["x*137.5","0.05*SQRT(x)"].toframe()'''<br><br/> | ||
[[File:Exp.JPG]]<br><br><br/> | [[File:Exp.JPG]]<br><br><br/> | ||
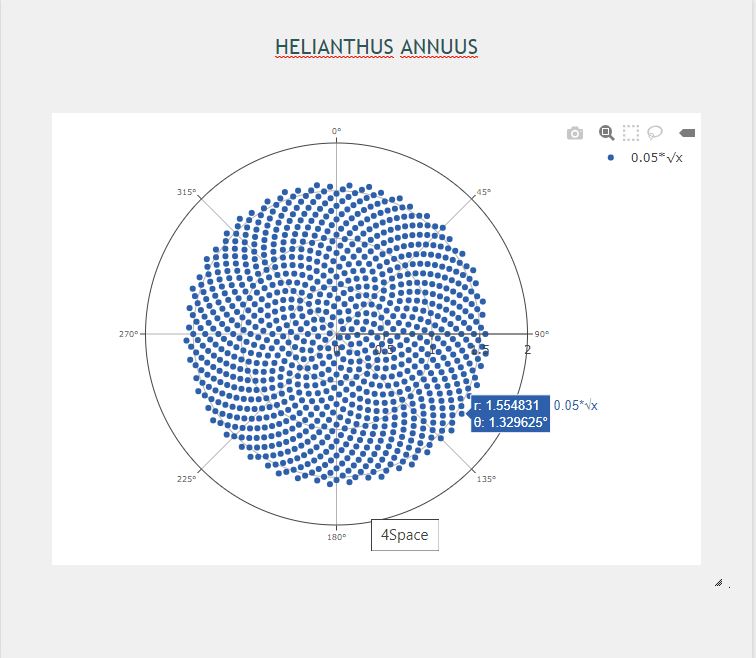
| − | ==='''PLOT | + | ==='''PLOT'''=== |
| + | '''Plot using the POLAR graph:'''<br><br/> | ||
[[File:Heli.JPG]]<br><br/> | [[File:Heli.JPG]]<br><br/> | ||
[[GRAPHING|'''''GRAPHING MAIN PAGE''''']] | [[GRAPHING|'''''GRAPHING MAIN PAGE''''']] | ||
Latest revision as of 13:16, 16 June 2020
HELIANTHUS ANNUUS
DESCRIPTION
In Polar Charts, a series is represented by a closed curve that connects points in the polar coordinate system.
Each data point is determined by the distance from the pole (the radial coordinate) and the angle from the fixed direction (the angular coordinate).
- Graphing a point with polar coordinates (r, θ).
- In polar coordinates, the dependent variable, r, gives not a height but a distance from the pole in direction θ.
- When graphing an equation in polar coordinates, we think of sweeping around the pole in the counterclockwise direction, and at each angle θ, the r-value tells us how far the graph is from the pole.
MODEL
A model for the pattern of florets in the head of a sunflower was proposed by H. Vogel in 1979.
This is expressed in polar coordinates:
where θ is the angle
r is the radius or distance from the center
n is the index number of the floret
c is a constant scaling factor
- It is a form of Fermat's spiral.
- The angle 137.5° is related to the golden ratio (55/144 of a circular angle, where 55 and 144 are Fibonacci numbers) and gives a close packing of florets.
EXPRESSION
Expression used in plotting:
Plotting from n = 1 to 1000,
(1..1000)@["x*137.5","0.05*SQRT(x)"].toframe()
PLOT
Plot using the POLAR graph:
GRAPHING MAIN PAGE