Difference between revisions of "Manuals/calci/HARMEAN"
Jump to navigation
Jump to search
| (19 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''HARMEAN( | + | <div style="font-size:30px">'''HARMEAN()'''</div><br/> |
| − | * | + | *Parameters are any set of positive real numbers. |
| + | **HARMEAN(), returns values along an exponential trend. | ||
| + | |||
==Description== | ==Description== | ||
*This function gives the Harmonic Mean of a given set of numbers. | *This function gives the Harmonic Mean of a given set of numbers. | ||
*Harmonic mean is used to calculate the average of a set of numbers. | *Harmonic mean is used to calculate the average of a set of numbers. | ||
*The Harmonic mean is always the lowest mean. | *The Harmonic mean is always the lowest mean. | ||
| − | *Normally <math>Harmonic mean < | + | *Normally <math>Harmonic mean < Geometric mean < Arithmetic mean</math> |
*Harmonic mean is defined as the reciprocal of the arithmetic mean by the reciprocals of a specified set of numbers. | *Harmonic mean is defined as the reciprocal of the arithmetic mean by the reciprocals of a specified set of numbers. | ||
| − | *The harmonic mean of a positive real numbers <math> | + | *The harmonic mean of a positive real numbers <math>x_1,x_2,x_3....x_n > 0</math> is defined by : |
| − | <math>H=\frac {n}{(1/ | + | <math>H=\frac {n}{(1/x_1+1/x_2+...+1/x_n)} </math> |
ie | ie | ||
:<math> H=\frac{n}{\sum_{i=1}^{n} \frac{1}{xi}}</math>. | :<math> H=\frac{n}{\sum_{i=1}^{n} \frac{1}{xi}}</math>. | ||
| − | *In HARMEAN( | + | *In <math>HARMEAN(),</math> Parameters are any positive real numbers, and here First Parameter is required. From the second parameter are optional. |
*Also arguments can be numbers,names, arrays or references that contain numbers. | *Also arguments can be numbers,names, arrays or references that contain numbers. | ||
*We can give logical values and text representations of numbers directly. | *We can give logical values and text representations of numbers directly. | ||
*Suppose the arguments contains any text, logical values or empty cells like that values are ignored. | *Suppose the arguments contains any text, logical values or empty cells like that values are ignored. | ||
*This will give the result as error when | *This will give the result as error when | ||
| − | 1. | + | 1.The arguments with the error values or the referred text couldn't translated in to numbers. |
2.Also any data <math>point \le 0</math>. | 2.Also any data <math>point \le 0</math>. | ||
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate HARMEAN in ZOS is <math>HARMEAN()</math>. | ||
| + | **Parameters are any set of positive real numbers. | ||
| + | *For e.g.,HARMEAN(20..30,11..15,45.1..56.1..0.5) | ||
| + | {{#ev:youtube|oHiCLVUJz-4|280|center|Harmonic Mean}} | ||
==Examples== | ==Examples== | ||
| − | #HARMEAN(1,2,3,4,5)=2.18978102189781 | + | #=HARMEAN(1,2,3,4,5) = 2.18978102189781 |
| − | #HARMEAN(20,25,32,41)=27.4649361523969 | + | #=HARMEAN(20,25,32,41) = 27.4649361523969 |
| − | #HARMEAN(0.25,5.4,3.7,10.1,15.2)=1.0821913906985883 | + | #=HARMEAN(0.25,5.4,3.7,10.1,15.2) = 1.0821913906985883 |
| − | #HARMEAN(3,5,0,2)= | + | #=HARMEAN(3,5,0,2) = #N/A (NUMBER > 0 REQUIRED) |
| − | #HARMEAN(1,-2,4)= | + | #=HARMEAN(1,-2,4) = #N/A (NUMBER > 0 REQUIRED) |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|X3nQMiBK9rc|280|center|Harmonic Mean}} | ||
==See Also== | ==See Also== | ||
| Line 31: | Line 43: | ||
*[[Manuals/calci/GEOMEAN | GEOMEAN ]] | *[[Manuals/calci/GEOMEAN | GEOMEAN ]] | ||
| + | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Harmonic_mean Harmonic mean] | ||
| − | + | ||
| − | [ | + | |
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 05:03, 12 August 2020
HARMEAN()
- Parameters are any set of positive real numbers.
- HARMEAN(), returns values along an exponential trend.
Description
- This function gives the Harmonic Mean of a given set of numbers.
- Harmonic mean is used to calculate the average of a set of numbers.
- The Harmonic mean is always the lowest mean.
- Normally
- Harmonic mean is defined as the reciprocal of the arithmetic mean by the reciprocals of a specified set of numbers.
- The harmonic mean of a positive real numbers is defined by :
ie
- .
- In Parameters are any positive real numbers, and here First Parameter is required. From the second parameter are optional.
- Also arguments can be numbers,names, arrays or references that contain numbers.
- We can give logical values and text representations of numbers directly.
- Suppose the arguments contains any text, logical values or empty cells like that values are ignored.
- This will give the result as error when
1.The arguments with the error values or the referred text couldn't translated in to numbers. 2.Also any data .
ZOS
- The syntax is to calculate HARMEAN in ZOS is .
- Parameters are any set of positive real numbers.
- For e.g.,HARMEAN(20..30,11..15,45.1..56.1..0.5)
Examples
- =HARMEAN(1,2,3,4,5) = 2.18978102189781
- =HARMEAN(20,25,32,41) = 27.4649361523969
- =HARMEAN(0.25,5.4,3.7,10.1,15.2) = 1.0821913906985883
- =HARMEAN(3,5,0,2) = #N/A (NUMBER > 0 REQUIRED)
- =HARMEAN(1,-2,4) = #N/A (NUMBER > 0 REQUIRED)
Related Videos
See Also
References
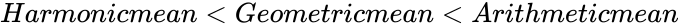
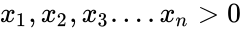 is defined by :
is defined by :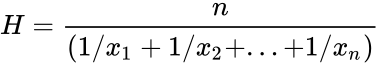 ie
ie
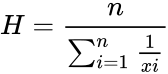 .
.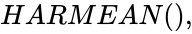 Parameters are any positive real numbers, and here First Parameter is required. From the second parameter are optional.
Parameters are any positive real numbers, and here First Parameter is required. From the second parameter are optional.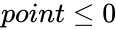 .
.
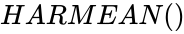 .
.