Difference between revisions of "Fisher's Exact Test"
Jump to navigation
Jump to search
| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:25px">'''FISHERSEXACTTEST(DataRange,NewTableFlag)'''</div | + | <div style="font-size:25px">'''FISHERSEXACTTEST(DataRange, NewTableFlag)'''</div> |
| − | *<math>DataRange</math> is the array of x and y values. | + | *'''<math>DataRange</math> is the array of x and y values. |
| − | *<math>NewTableFlag</math> is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube. | + | *'''<math>NewTableFlag</math> is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.<br></br> |
| − | == | + | ==='''DESCRIPTION=== |
| − | * This function gives the test statistic of the Fisher's Exact Test. | + | * '''This function gives the test statistic of the Fisher's Exact Test. |
| − | * Since this method is more computationally intense, it is best used for smaller samples. | + | * '''Since this method is more computationally intense, it is best used for smaller samples. |
| − | * Like the chi-square test for (2x2) tables, Fisher's exact test examines the relation between two dimensions of the table (classification into rows vs. columns). | + | * '''Like the chi-square test for (2x2) tables, Fisher's exact test examines the relation between two dimensions of the table (classification into rows vs. columns). |
| − | * For experiments with small numbers of participants (below 1,000), Fisher’s is more accurate than the chi-square test or G-test. | + | * '''For experiments with small numbers of participants (below 1,000), Fisher’s is more accurate than the chi-square test or G-test. |
| − | * The null hypothesis is that these two classifications are not different. | + | * '''The null hypothesis is that these two classifications are not different. |
| − | * The P values in this test are computed by considering all possible tables that could give the row and column totals observed. | + | * '''The P values in this test are computed by considering all possible tables that could give the row and column totals observed.<br></br> |
| − | == | + | ==='''ASSUMPTIONS=== |
| − | * Unlike other statistical tests, there isn’t a formula for Fisher’s. | + | * '''Unlike other statistical tests, there isn’t a formula for Fisher’s. |
| − | * To get a result for this test, calculate the probability of getting the observed data using the null hypothesis that the proportions are the same for both sets. | + | * '''To get a result for this test, calculate the probability of getting the observed data using the null hypothesis that the proportions are the same for both sets.<br></br> |
| − | == | + | ==='''EXAMPLE=== |
{| class="wikitable" | {| class="wikitable" | ||
| − | |+ | + | |+SPREADSHEET |
|- | |- | ||
! !! A !! B | ! !! A !! B | ||
| Line 27: | Line 27: | ||
| 8 || 9 | | 8 || 9 | ||
|} | |} | ||
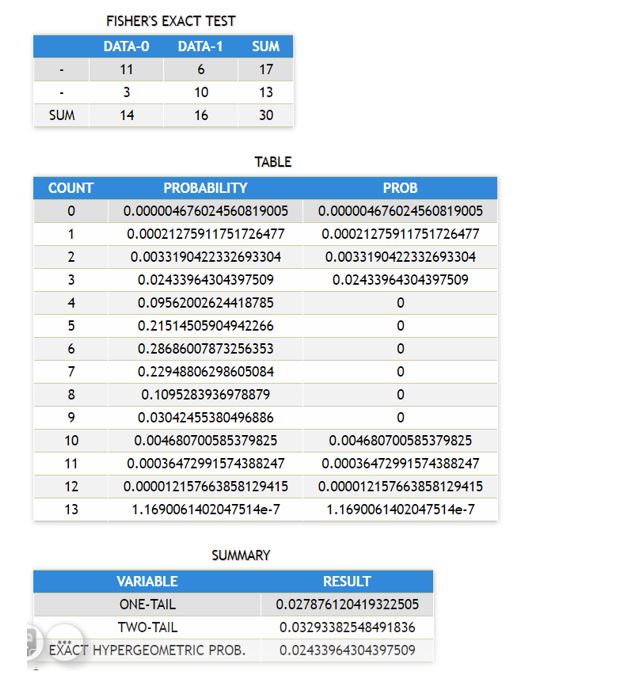
| − | =FISHERSEXACTTEST([A1:B2],true) | + | ='''FISHERSEXACTTEST([A1:B2], true) |
{| class="wikitable" | {| class="wikitable" | ||
| Line 38: | Line 38: | ||
| || 8 || 9 || 17 | | || 8 || 9 || 17 | ||
|- | |- | ||
| − | |SUM || 13 || 12 || 25 | + | |'''SUM''' || 13 || 12 || 25 |
|} | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+TABLE | ||
| + | |- | ||
| + | ! COUNT !! PROBABILITY !! PROB | ||
| + | |- | ||
| + | | 0 || 0.0011899313501144164 || 0.0011899313501144164 | ||
| + | |- | ||
| + | | 1 || 0.019038901601830662 || 0.019038901601830662 | ||
| + | |- | ||
| + | | 2 || 0.10471395881006865 || 0.10471395881006865 | ||
| + | |- | ||
| + | | 3 || 0.2617848970251716 || 0.2617848970251716 | ||
| + | |- | ||
| + | | 4 || 0.32723112128146453 || 0 | ||
| + | |- | ||
| + | | 5 || 0.2094279176201373 || 0.2094279176201373 | ||
| + | |- | ||
| + | | 6 || 0.06663615560640732 || 0.06663615560640732 | ||
| + | |- | ||
| + | | 7 || 0.009519450800915331 || 0.009519450800915331 | ||
| + | |- | ||
| + | | 8 || 0.0004576659038901602 || 0.0004576659038901602 | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+SUMMARY | ||
| + | |- | ||
| + | ! VARIABLE !! RESULT | ||
| + | |- | ||
| + | | ONE-TAIL || 0.38672768878718533 | ||
| + | |- | ||
| + | | TWO-TAIL || 0.6727688787185354 | ||
| + | |- | ||
| + | | EXACT HYPERGEOMETRIC PROB. || 0.2617848970251716 | ||
| + | |} | ||
| + | <br></br> | ||
| + | |||
| + | ==='''Comparison of software=== | ||
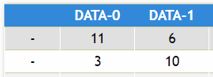
| + | '''Conduct Fisher's exact test for the data in the range B2:C4.<br><br> | ||
| + | [[File:fish.JPG]]<br><br> | ||
| + | |||
| + | '''SOLUTION'''<br> | ||
| + | '''In z3:'''<br> | ||
| + | [[File:fishz.JPG]]<br><br> | ||
| + | |||
| + | '''In R:'''<br> | ||
| + | [[File:fishr.JPG]]<br><br> | ||
Latest revision as of 09:26, 19 August 2020
FISHERSEXACTTEST(DataRange, NewTableFlag)
- is the array of x and y values.
- is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
DESCRIPTION
- This function gives the test statistic of the Fisher's Exact Test.
- Since this method is more computationally intense, it is best used for smaller samples.
- Like the chi-square test for (2x2) tables, Fisher's exact test examines the relation between two dimensions of the table (classification into rows vs. columns).
- For experiments with small numbers of participants (below 1,000), Fisher’s is more accurate than the chi-square test or G-test.
- The null hypothesis is that these two classifications are not different.
- The P values in this test are computed by considering all possible tables that could give the row and column totals observed.
ASSUMPTIONS
- Unlike other statistical tests, there isn’t a formula for Fisher’s.
- To get a result for this test, calculate the probability of getting the observed data using the null hypothesis that the proportions are the same for both sets.
EXAMPLE
| A | B | |
|---|---|---|
| 1 | 5 | 3 |
| 2 | 8 | 9 |
=FISHERSEXACTTEST([A1:B2], true)
| DATA-0 | DATA-1 | SUM | |
|---|---|---|---|
| 5 | 3 | 8 | |
| 8 | 9 | 17 | |
| SUM | 13 | 12 | 25 |
| COUNT | PROBABILITY | PROB |
|---|---|---|
| 0 | 0.0011899313501144164 | 0.0011899313501144164 |
| 1 | 0.019038901601830662 | 0.019038901601830662 |
| 2 | 0.10471395881006865 | 0.10471395881006865 |
| 3 | 0.2617848970251716 | 0.2617848970251716 |
| 4 | 0.32723112128146453 | 0 |
| 5 | 0.2094279176201373 | 0.2094279176201373 |
| 6 | 0.06663615560640732 | 0.06663615560640732 |
| 7 | 0.009519450800915331 | 0.009519450800915331 |
| 8 | 0.0004576659038901602 | 0.0004576659038901602 |
| VARIABLE | RESULT |
|---|---|
| ONE-TAIL | 0.38672768878718533 |
| TWO-TAIL | 0.6727688787185354 |
| EXACT HYPERGEOMETRIC PROB. | 0.2617848970251716 |
Comparison of software
Conduct Fisher's exact test for the data in the range B2:C4.
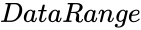 is the array of x and y values.
is the array of x and y values.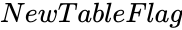 is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.