Difference between revisions of "Manuals/calci/CHIINV"
Jump to navigation
Jump to search
| (22 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''CHIINV( | + | <div style="font-size:30px">'''CHIINV (probability,degrees_freedom,Accuracy,DivisionDepthArray)'''</div><br/> |
| − | *Where | + | *Where <math>probability</math> is the value associated with the Chi-squared Distribution |
| + | *<math>degrees freedom</math> is the number of Degrees of Freedom. | ||
| + | *<math>Accuracy</math> is the correct decimal places of the result. | ||
| + | **CHIINV(), returns the inverse of the one-tailed probability of the chi-squared distribution. | ||
| + | |||
==Description== | ==Description== | ||
| − | *This function gives the inverse value of | + | *This function gives the inverse value of One_tailed probability of the Chi-squared Distribution. |
| − | *It is called | + | *It is called Inverted-Chi-square Distribution and it is a Continuous Probability Distribution of a positive-valued random variable. |
| − | + | ||
| − | *Degrees of freedom=(r-1)(c-1). | + | *Degrees of freedom <math>df</math>=<math>(r-1)(c-1)</math>. |
| − | *The | + | *The <math>\chi^2</math> static used to compare the observed value in each table to the value which would be the expected under the assumption. |
| − | *If X has the chi-squared distribution with | + | *If <math>X</math> has the chi-squared distribution with n degrees of freedom, then according to the definition, <math>\frac{1}{X}</math> has the Inverse-chi-squared distribution with <math>n</math> degrees of freedom; |
| − | *CHIINV | + | *If <math>CHIDIST (Number,DegreeOfFreedom)=probability</math>, then <math>CHIINV (probability,degrees freedom,Accuracy,DivisionDepthArray)= Number</math>. |
| + | *CHIINV use the iterating method to find the value of <math>x</math>.suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
*This function will give the error result when | *This function will give the error result when | ||
| − | + | 1.Any one of the arguments are non-numeric | |
| − | + | 2.degrees freedom value is not an integer | |
| − | + | 3.degrees freedom < 1 or degrees freedom><math>10^{10}</math> | |
| − | + | 4.Also probability < 0 or probability>1. | |
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate CHIINV in ZOS is <math>CHIINV (probability,degrees_freedom,Accuracy,DivisionDepthArray)</math>. | ||
| + | **Where <math>probability</math> is the value associated with the Chi-squared Distribution | ||
| + | **<math>degrees freedom</math> is the number of Degrees of Freedom | ||
| + | *For e.g.,CHIINV(0.0257,3) | ||
| + | {{#ev:youtube|sfB2dLFPu1U|280|center|Inverse Chi-Squared Distribution}} | ||
==Examples== | ==Examples== | ||
| − | #CHIINV(0.0001234098,2)=18 | + | #CHIINV(0.0001234098,2) = 18 |
| − | #CHIINV(0.2547876,5)=6. | + | #CHIINV(0.2547876,5) = 6.5669999999999655 |
| − | #CHIINV(0.157299207050,1)= | + | #CHIINV(0.157299207050,1) = 1.9991000000000005 |
| − | #CHIINV(0.6785412,-1)= | + | #CHIINV(0.6785412,-1) = #N/A (DEGREESOFFREEDOM < 1) |
| + | |||
| + | ==Related Videos== | ||
| + | {{#ev:youtube|UPawNLQOv-8|280|center|Chi-Square Test}} | ||
| + | |||
==See Also== | ==See Also== | ||
*[[Manuals/calci/CHIDIST | CHIDIST ]] | *[[Manuals/calci/CHIDIST | CHIDIST ]] | ||
| Line 27: | Line 43: | ||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/ | + | [http://en.wikipedia.org/wiki/Inverse-chi-squared_distribution| Inverse-chi-squared Distribution] |
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 03:22, 25 August 2020
CHIINV (probability,degrees_freedom,Accuracy,DivisionDepthArray)
- Where is the value associated with the Chi-squared Distribution
- is the number of Degrees of Freedom.
- is the correct decimal places of the result.
- CHIINV(), returns the inverse of the one-tailed probability of the chi-squared distribution.
Description
- This function gives the inverse value of One_tailed probability of the Chi-squared Distribution.
- It is called Inverted-Chi-square Distribution and it is a Continuous Probability Distribution of a positive-valued random variable.
- Degrees of freedom =.
- The static used to compare the observed value in each table to the value which would be the expected under the assumption.
- If has the chi-squared distribution with n degrees of freedom, then according to the definition, has the Inverse-chi-squared distribution with degrees of freedom;
- If , then .
- CHIINV use the iterating method to find the value of .suppose the iteration has not converged after 100 searches, then the function gives the error result.
- This function will give the error result when
1.Any one of the arguments are non-numeric 2.degrees freedom value is not an integer 3.degrees freedom < 1 or degrees freedom> 4.Also probability < 0 or probability>1.
ZOS
- The syntax is to calculate CHIINV in ZOS is .
- Where is the value associated with the Chi-squared Distribution
- is the number of Degrees of Freedom
- For e.g.,CHIINV(0.0257,3)
Examples
- CHIINV(0.0001234098,2) = 18
- CHIINV(0.2547876,5) = 6.5669999999999655
- CHIINV(0.157299207050,1) = 1.9991000000000005
- CHIINV(0.6785412,-1) = #N/A (DEGREESOFFREEDOM < 1)
Related Videos
See Also
References
Inverse-chi-squared Distribution
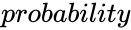 is the value associated with the Chi-squared Distribution
is the value associated with the Chi-squared Distribution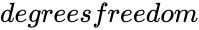 is the number of Degrees of Freedom.
is the number of Degrees of Freedom.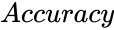 is the correct decimal places of the result.
is the correct decimal places of the result.
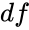 =
=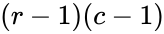 .
.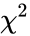 static used to compare the observed value in each table to the value which would be the expected under the assumption.
static used to compare the observed value in each table to the value which would be the expected under the assumption.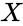 has the chi-squared distribution with n degrees of freedom, then according to the definition,
has the chi-squared distribution with n degrees of freedom, then according to the definition, 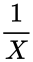 has the Inverse-chi-squared distribution with
has the Inverse-chi-squared distribution with  degrees of freedom;
degrees of freedom;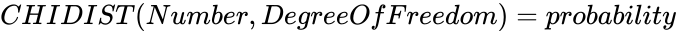 , then
, then 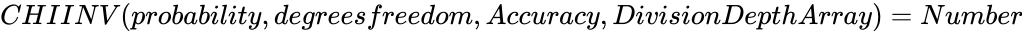 .
. .suppose the iteration has not converged after 100 searches, then the function gives the error result.
.suppose the iteration has not converged after 100 searches, then the function gives the error result.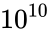 4.Also probability < 0 or probability>1.
4.Also probability < 0 or probability>1.
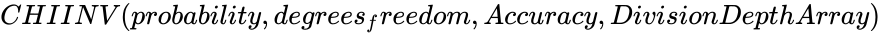 .
.