Difference between revisions of "Manuals/calci/CORREL"
Jump to navigation
Jump to search
| (32 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''CORREL( | + | <div style="font-size:30px">'''CORREL(Array1,Array2)'''</div><br/> |
| − | *<math> | + | *<math>Array1</math> and <math>Array2 </math> are the set of values. |
| + | **CORREL(), returns the correlation coefficient between two data sets. | ||
| + | |||
==Description== | ==Description== | ||
| − | *This function gives the correlation coefficient of the 1st set( | + | *This function gives the correlation coefficient of the 1st set(<math>Array1</math>) of values and 2nd set(<math>Array2</math>) of values. |
*Correlation is a statistical technique which shows the relation of strongly paired variables. | *Correlation is a statistical technique which shows the relation of strongly paired variables. | ||
| − | *For example ,test average and study time are related;those who spending time | + | *For example, test average and study time are related; those who spending more time to study will get high marks and Average will go down for those who spend less time for studies. |
| − | *There are different correlation techniques | + | *There are different correlation techniques to measure the Degree of Correlation. |
| − | *The most common of these is the Pearson | + | *The most common of these is the Pearson Correlation Coefficient denoted by <math>r_{xy}</math>. |
| − | *The main result of a correlation is called the | + | *The main result of a correlation is called the Correlation Coefficient(<math>r</math>)which ranges from -1 to +1. |
| − | *The r value is positive i.e | + | *The correlation calculation only works well for relationships that follow a straight line. |
| − | *The r value is negative i.e. (-1) when one value decreases as the other increases then it is called | + | *The <math>r</math> value is positive i.e +1 when the two set values increase together then it is the perfect Positive Correlation. |
| − | *Suppose the r value is 0 | + | *The <math>r</math> value is negative i.e. (-1) when one value decreases as the other increases then it is called Negative Correlation. |
| − | *If we have a series of n measurements of X and Y written as | + | *Suppose the <math>r</math> value is 0 then there is no correlation (the values don't seem linked at all). |
| − | + | *If we have a series of <math>n</math> measurements of <math>X</math> and <math>Y</math> written as <math>x_i</math> and <math>y_i</math> where <math>i = 1, 2,...n</math> then the Sample Correlation Coefficient is: | |
| − | + | <math>CORREL(X,Y)= r_{xy}= \frac{\sum_{i=1}^n (x_i-\bar x)(y_i-\bar y)}{\sqrt{ \sum_{i=1}^n (x_i-\bar x)^2 \sum_{i=1}^n (y_i-\bar y)^2}}</math> | |
| − | + | *<math>\bar x</math> and <math>\bar y</math> are the sample means of <math>X</math> and <math>Y</math>. | |
| − | *Suppose | + | *This function will give the result as error when |
| + | 1.<math>Array1</math> and <math>Array2</math> are non-numeric or different number of data points. | ||
| + | 2.<math>Array1</math> or <math>Array2</math> is empty | ||
| + | 3.The denominator value is zero. | ||
| + | *Suppose <math>Array1</math> and <math>Array2</math> contains any text, logical values, or empty cells, like that values are ignored. | ||
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate CORREL in ZOS is <math>CORREL(Array1,Array2)</math>. | ||
| + | **<math>Array1</math> and <math>Array2 </math> are the set of values. | ||
| + | *For e.g.,CORREL([(-5)..(-1)],[10..15]) | ||
| + | {{#ev:youtube|Il4jCpJy0IA|280|center|Correlation Coefficient}} | ||
==Examples== | ==Examples== | ||
| − | + | 1. Find the correlation coefficients for X and Y values are given below :X={1,2,3,4,5}; Y={11,22,34,43,56} | |
| − | CORREL(A4:A8,B4:B8)=0.99890610723867 | + | |
| − | + | =CORREL(A4:A8,B4:B8)=0.99890610723867 | |
| − | + | ||
| + | 2. The following table gives the math scores and times taken to run 100 m for 10 friends:SCORE(X)={52,25,35,90,76,40}; TIME TAKEN(Y)={11.3,12.9,11.9,10.2,11.1,12.5} | ||
| + | |||
| + | =CORREL(A5:A10,B5:B10)= -0.93626409417769 | ||
| + | |||
| + | 3. Find the correlation coefficients for X and Y values are given below :X={-4,11,34,87};Y={9,2,59,24} | ||
| + | |||
| + | =CORREL(A1:A4,B1:B4)=0.353184665607273 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|s2TVkYmmCAs|280|center|Correlation Coefficient}} | ||
==See Also== | ==See Also== | ||
*[[Manuals/calci/COVAR | COVAR ]] | *[[Manuals/calci/COVAR | COVAR ]] | ||
*[[Manuals/calci/FISHER | FISHER ]] | *[[Manuals/calci/FISHER | FISHER ]] | ||
| + | |||
| + | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient Correlation] | ||
| − | + | ||
| − | [ | + | *[[Z_API_Functions | List of Main Z Functions]] |
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 04:26, 25 August 2020
CORREL(Array1,Array2)
- and are the set of values.
- CORREL(), returns the correlation coefficient between two data sets.
Description
- This function gives the correlation coefficient of the 1st set() of values and 2nd set() of values.
- Correlation is a statistical technique which shows the relation of strongly paired variables.
- For example, test average and study time are related; those who spending more time to study will get high marks and Average will go down for those who spend less time for studies.
- There are different correlation techniques to measure the Degree of Correlation.
- The most common of these is the Pearson Correlation Coefficient denoted by .
- The main result of a correlation is called the Correlation Coefficient()which ranges from -1 to +1.
- The correlation calculation only works well for relationships that follow a straight line.
- The value is positive i.e +1 when the two set values increase together then it is the perfect Positive Correlation.
- The value is negative i.e. (-1) when one value decreases as the other increases then it is called Negative Correlation.
- Suppose the value is 0 then there is no correlation (the values don't seem linked at all).
- If we have a series of measurements of and written as and where then the Sample Correlation Coefficient is:
- and are the sample means of and .
- This function will give the result as error when
1. and are non-numeric or different number of data points. 2. or is empty 3.The denominator value is zero.
- Suppose and contains any text, logical values, or empty cells, like that values are ignored.
ZOS
- The syntax is to calculate CORREL in ZOS is .
- and are the set of values.
- For e.g.,CORREL([(-5)..(-1)],[10..15])
Examples
1. Find the correlation coefficients for X and Y values are given below :X={1,2,3,4,5}; Y={11,22,34,43,56}
=CORREL(A4:A8,B4:B8)=0.99890610723867
2. The following table gives the math scores and times taken to run 100 m for 10 friends:SCORE(X)={52,25,35,90,76,40}; TIME TAKEN(Y)={11.3,12.9,11.9,10.2,11.1,12.5}
=CORREL(A5:A10,B5:B10)= -0.93626409417769
3. Find the correlation coefficients for X and Y values are given below :X={-4,11,34,87};Y={9,2,59,24}
=CORREL(A1:A4,B1:B4)=0.353184665607273
Related Videos
See Also
References
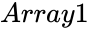 and
and 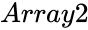 are the set of values.
are the set of values.
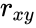 .
.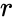 )which ranges from -1 to +1.
)which ranges from -1 to +1. measurements of
measurements of 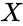 and
and 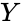 written as
written as 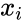 and
and 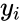 where
where 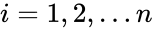 then the Sample Correlation Coefficient is:
then the Sample Correlation Coefficient is: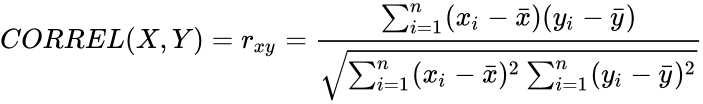
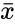 and
and 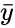 are the sample means of
are the sample means of 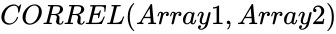 .
.