Difference between revisions of "Manuals/calci/ERFC"
Jump to navigation
Jump to search
| (9 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''ERFC( | + | <div style="font-size:30px">'''ERFC(a,accuracy)'''</div><br/> |
| − | *<math> | + | *<math>a</math> is the lower limit. |
| + | *<math>accuracy</math> gives the accurate value of the solution. | ||
| + | **ERFC(),returns the Complementary Error Function | ||
| + | |||
==Description== | ==Description== | ||
| Line 8: | Line 11: | ||
*ERFC is defined by: | *ERFC is defined by: | ||
<math>ERFC(x)=\frac{2}{\sqrt{\pi}}\int\limits_{x}^{\infty}e^{-t^2} dt=1-ERF(x)</math>. | <math>ERFC(x)=\frac{2}{\sqrt{\pi}}\int\limits_{x}^{\infty}e^{-t^2} dt=1-ERF(x)</math>. | ||
| − | *This function will return the result as error when | + | *This function will return the result as error when a is nonnumeric or negative. |
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate complementary error function in ZOS is <math>ERFC(a,accuracy)</math>. | ||
| + | **<math>a</math> is the lower limit. | ||
| + | **<math>accuracy</math> gives the accurate value of the solution. | ||
| + | *For e.g.,ERFC(10),ERFC(10,0.01) | ||
==Examples== | ==Examples== | ||
| − | #ERFC(3)=0. | + | #ERFC(3)=0.000022090496998639075 |
| − | #ERFC(2)=0. | + | #ERFC(2)=0.004677734981047288 |
#ERFC(0)=1 | #ERFC(0)=1 | ||
| − | #ERFC(-2)= | + | #ERFC(-2)=1.9953222650189528 |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|PBSFXukqztU|280|center|Complimentary Error Function}} | ||
==See Also== | ==See Also== | ||
| Line 20: | Line 33: | ||
==References== | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Error_function Error Function ] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 03:14, 29 September 2021
ERFC(a,accuracy)
- is the lower limit.
- gives the accurate value of the solution.
- ERFC(),returns the Complementary Error Function
Description
- This function gives the complementary ERF function.
- The complementary error function is the error function with the limit x and infinity. It is denoted by erfc(x).
- It is also called scaled complementary error function.
- ERFC is defined by:
.
- This function will return the result as error when a is nonnumeric or negative.
ZOS
- The syntax is to calculate complementary error function in ZOS is .
- is the lower limit.
- gives the accurate value of the solution.
- For e.g.,ERFC(10),ERFC(10,0.01)
Examples
- ERFC(3)=0.000022090496998639075
- ERFC(2)=0.004677734981047288
- ERFC(0)=1
- ERFC(-2)=1.9953222650189528
Related Videos
See Also
References
 is the lower limit.
is the lower limit. gives the accurate value of the solution.
gives the accurate value of the solution.
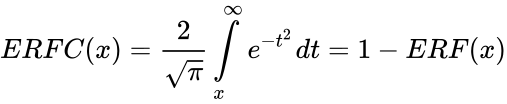 .
.
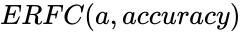 .
.