Difference between revisions of "Manuals/calci/TETRATE"
Jump to navigation
Jump to search
| (27 intermediate revisions by 2 users not shown) | |||
| Line 8: | Line 8: | ||
*The hyperoperation after exponentiation is Tetration. | *The hyperoperation after exponentiation is Tetration. | ||
*Tetration is called iterated exponentiation. | *Tetration is called iterated exponentiation. | ||
| − | *The notation <math>^n a</math> means <math> a^ | + | *The notation <math>^n{a}</math> means <math> a^{a^{a}}</math> the application of exponentiation <math> n-1</math> times. |
| − | + | *For any positive real a>0 and non-negative integer <math>n\ge 0</math> we define <math>^n{a}</math>by: | |
| − | * | + | <math>^n{a} = |
| − | <math> | + | \begin{cases} |
| − | + | 1, & \mbox{if }n\mbox{ =0} \\ | |
| − | * | + | a^{a^{(n-1)}}, & \mbox{if }n\mbox{ >0} \\ |
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | ==Examples== | ||
| + | #TETRATE (3,2) = 27 | ||
| + | #TETRATE (4,3) = 1.3407807929942597e+154 | ||
| + | #TETRATE (10,2) = 10000000000 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=kITJ6qH7jS0|280|center|Exponent}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/SLOG| SLOG]] | ||
| + | *[[Manuals/calci/SUPERLOGARITHM| SUPERLOGARITHM]] | ||
| + | *[[Manuals/calci/TETRA| TETRA]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Tetration Tetration] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 04:34, 27 May 2022
TETRATE(a,n)
- is the base value.
- is power value.
Description
- This function shows the tetration value of the given number.
- In , is the base value and is the power value.
- The hyperoperation after exponentiation is Tetration.
- Tetration is called iterated exponentiation.
- The notation means the application of exponentiation times.
- For any positive real a>0 and non-negative integer we define by:
Failed to parse (unknown function "\begin{cases}"): {\displaystyle ^n{a} = \begin{cases} 1, & \mbox{if }n\mbox{ =0} \\ a^{a^{(n-1)}}, & \mbox{if }n\mbox{ >0} \\ \end{cases} }
Examples
- TETRATE (3,2) = 27
- TETRATE (4,3) = 1.3407807929942597e+154
- TETRATE (10,2) = 10000000000
Related Videos
See Also
References
 is the base value.
is the base value. is power value.
is power value.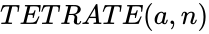 ,
,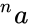 means
means 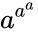 the application of exponentiation
the application of exponentiation  times.
times.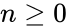 we define
we define