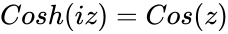Difference between revisions of "Manuals/calci/COSH"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
* Here <math>COSH=\frac{e^z+e^{-z}}{2}</math> or <math>-COS(iz)</math>, where <math>i</math> is the imaginary unit and <math>i=\sqrt{-1}</math> | * Here <math>COSH=\frac{e^z+e^{-z}}{2}</math> or <math>-COS(iz)</math>, where <math>i</math> is the imaginary unit and <math>i=\sqrt{-1}</math> | ||
*Also relation between Hyperbolic & Trigonometric function is <math>Cos(iz)=Cos(hz)</math> & <math>Cosh(iz)= Cos(z)</math> | *Also relation between Hyperbolic & Trigonometric function is <math>Cos(iz)=Cos(hz)</math> & <math>Cosh(iz)= Cos(z)</math> | ||
| − | *COSH(-z)=COSH(z) | + | *COSH(-z) = COSH(z) |
== Examples == | == Examples == | ||
Revision as of 05:48, 5 November 2013
COSH(z)
- where z is any real number
Description
- This function gives the hyperbolic Cos of 'z'.
- Also it is called as Circular function.
- Here or , where is the imaginary unit and
- Also relation between Hyperbolic & Trigonometric function is &
- COSH(-z) = COSH(z)
Examples
COSH(z)
- z is any real number.
| COSH(z) | Value(Radian) |
| COSH(0) | 1 |
| COSH(10) | 11013.232920103319 |
| COSH(7) | COSH(7)=548.3170352 |
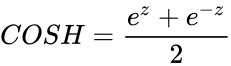 or
or 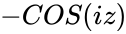 , where
, where 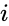 is the imaginary unit and
is the imaginary unit and 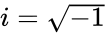
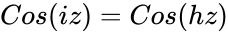 &
&