Difference between revisions of "Manuals/calci/EXPONDIST"
Jump to navigation
Jump to search
| (31 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size: | + | <div style="font-size:25px">'''EXPONDIST(X,Lambda,Cumulative)'''</div><br/> |
| − | *<math> | + | *<math>X</math> is the value of the function. |
| − | *<math>lambda</math> is the value of the rate parameter | + | *<math>Lambda(\lambda)</math> is the value of the rate parameter. |
| − | *<math> | + | *<math>Cumulative</math> is the logical value like TRUE or FALSE. |
| + | **EXPONDIST(), returns the exponential distribution. | ||
==Description== | ==Description== | ||
| − | + | *This function gives the Exponential Distribution. This distribution is used to model the time until something happens in the process. | |
| − | *This function gives the Exponential Distribution. This distribution used to model the time until something happens in the process. | ||
*This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate. | *This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate. | ||
*For e.g Time between successive vehicles arrivals at a workshop. | *For e.g Time between successive vehicles arrivals at a workshop. | ||
| − | *In EXPONDIST( | + | *Exponential distribution is the only continuous memoryless random distribution. It is a continuous analog of the Geometric distribution. |
| − | *Suppose we are not giving the | + | *In <math>EXPONDIST(X,Lambda,Cumulative)</math>, <math>X</math> is the value of the function, <math> Lambda</math> is called rate parameter and <math>Cumulative</math> is either TRUE or FALSE. |
| + | *This function will give the Cumulative Distribution Function when <math>Cumulative</math> is TRUE, otherwise it will give the Probability Density Function , when <math>Cumulative</math> is FALSE. | ||
| + | *Suppose we are not giving the <math>Cumulative</math> value, by default it will consider the <math>Cumulative</math> value is FALSE. | ||
*This function will give the error result when | *This function will give the error result when | ||
| − | 1. <math> | + | 1. <math>X</math> or <math>Lambda</math> is non-numeric. |
| − | 2. <math> | + | 2. <math>X<0</math> or <math>Lambda \le 0</math> |
| − | The Probability Density Function | + | The Probability Density Function of an Exponential Distribution is: |
| − | + | <math>f(x,\lambda)=\begin{cases} | |
| − | + | \lambda e^{-\lambda x} &, x \ge 0 \\ | |
| + | 0 &, x<0 | ||
| + | \end{cases}</math> | ||
or | or | ||
| − | :<math>f(x;\lambda)= | + | :<math>f(x;\lambda)= \lambda e^{-\lambda x} .H(x)</math> |
| − | *where <math>\lambda</math> is the rate parameter and H(x) is the Heaviside step function | + | *where <math>\lambda</math> is the rate parameter and <math>H(x)</math> is the Heaviside step function |
*This function is valid only on the interval [0,infinity]. | *This function is valid only on the interval [0,infinity]. | ||
The Cumulative Distribution Function is : | The Cumulative Distribution Function is : | ||
| − | <math>F(x | + | <math>F(x,\lambda)=\begin{cases} |
| − | + | 1-e^{-\lambda x} &, x \ge 0 \\ | |
| + | 0 &, x<0 | ||
| + | \end{cases}</math> | ||
or | or | ||
:<math>F(x,\lambda)=1-e^{-\lambda x}.H(x)</math> | :<math>F(x,\lambda)=1-e^{-\lambda x}.H(x)</math> | ||
| − | *The | + | ==ZOS== |
| − | * | + | *The syntax is to calculate EXPONDIST in ZOS is <math>(X,Lambda,Cumulative)</math>. |
| + | **where <math>X</math> is the value of the function | ||
| + | **<math>Lambda</math> is the value of the rate parameter | ||
| + | **<math>Cumulative</math> is the logical value like TRUE or FALSE. | ||
| + | *For e.g.,EXPONDIST(11..12,2.3..3.3..0.4,FALSE) | ||
| + | {{#ev:youtube|R1BjrD7T6Fs|280|center|Exponential Distribution}} | ||
==Examples== | ==Examples== | ||
| − | Question : If jobs arrive at an average of 15 seconds, | + | Question : If jobs arrive at an average of 15 seconds, <math>\lambda =5</math> per minute, what is the probability of waiting 30 seconds, i.e 0.5 min? |
| − | Here | + | Here <math>\lambda =5</math> and <math>x=0.5</math> |
| − | =EXPONDIST(0.5,5,TRUE)=0.917915001 | + | *=EXPONDIST(0.5,5,TRUE) = 0.917915001 |
| − | =EXPONDIST(5,3,TRUE)=0.999999694 | + | *=EXPONDIST(5,3,TRUE) = 0.999999694 |
| − | =EXPONDIST(0.4,2,FALSE)=0.898657928 | + | *=EXPONDIST(0.4,2,FALSE) = 0.898657928 |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|RQ9VOaWxDFo|280|center|Exponential Probability}} | ||
==See Also== | ==See Also== | ||
| Line 43: | Line 58: | ||
==References== | ==References== | ||
| − | *[http://en.wikipedia.org/wiki/Exponential_distribution Exponential Distribution] | + | *[http://en.wikipedia.org/wiki/Exponential_distribution Exponential Distribution] |
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:04, 10 August 2018
EXPONDIST(X,Lambda,Cumulative)
- is the value of the function.
- is the value of the rate parameter.
- is the logical value like TRUE or FALSE.
- EXPONDIST(), returns the exponential distribution.
Description
- This function gives the Exponential Distribution. This distribution is used to model the time until something happens in the process.
- This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate.
- For e.g Time between successive vehicles arrivals at a workshop.
- Exponential distribution is the only continuous memoryless random distribution. It is a continuous analog of the Geometric distribution.
- In , is the value of the function, is called rate parameter and is either TRUE or FALSE.
- This function will give the Cumulative Distribution Function when is TRUE, otherwise it will give the Probability Density Function , when is FALSE.
- Suppose we are not giving the value, by default it will consider the value is FALSE.
- This function will give the error result when
1. or is non-numeric. 2. or
The Probability Density Function of an Exponential Distribution is: or
- where is the rate parameter and is the Heaviside step function
- This function is valid only on the interval [0,infinity].
The Cumulative Distribution Function is : or
ZOS
- The syntax is to calculate EXPONDIST in ZOS is .
- where is the value of the function
- is the value of the rate parameter
- is the logical value like TRUE or FALSE.
- For e.g.,EXPONDIST(11..12,2.3..3.3..0.4,FALSE)
Examples
Question : If jobs arrive at an average of 15 seconds, per minute, what is the probability of waiting 30 seconds, i.e 0.5 min? Here and
- =EXPONDIST(0.5,5,TRUE) = 0.917915001
- =EXPONDIST(5,3,TRUE) = 0.999999694
- =EXPONDIST(0.4,2,FALSE) = 0.898657928
Related Videos
See Also
References
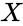 is the value of the function.
is the value of the function.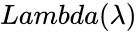 is the value of the rate parameter.
is the value of the rate parameter.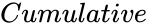 is the logical value like TRUE or FALSE.
is the logical value like TRUE or FALSE.
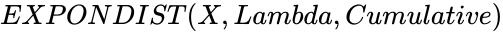 ,
, 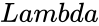 is called rate parameter and
is called rate parameter and 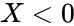 or
or 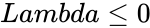
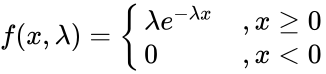 or
or
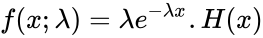
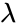 is the rate parameter and
is the rate parameter and 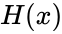 is the Heaviside step function
is the Heaviside step function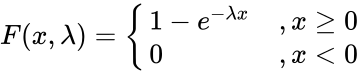 or
or
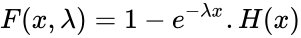
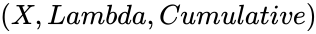 .
.
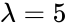 per minute, what is the probability of waiting 30 seconds, i.e 0.5 min?
Here
per minute, what is the probability of waiting 30 seconds, i.e 0.5 min?
Here