Difference between revisions of "Manuals/calci/REGRESSION"
| (25 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''REGRESSIONANALYSIS(y,x)'''</div><br/> | <div style="font-size:30px">'''REGRESSIONANALYSIS(y,x)'''</div><br/> | ||
| + | |||
| + | Regression analysis is a form of predictive modelling technique which investigates the relationship between a dependent (target) and independent variable (s) (predictor). This technique is used for forecasting, time series modelling and finding the causal effect relationship between the variables. | ||
| + | |||
| + | |||
*<math>y </math> is the set of dependent variables . | *<math>y </math> is the set of dependent variables . | ||
*<math>x </math> is the set of independent variables. | *<math>x </math> is the set of independent variables. | ||
| − | |||
==Description== | ==Description== | ||
*This function is calculating the Regression analysis of the given data. | *This function is calculating the Regression analysis of the given data. | ||
| − | *This analysis is very useful for the | + | *This analysis is very useful for the analyzing the large amounts of data and making predictions. |
*This analysis give the result in three table values. | *This analysis give the result in three table values. | ||
# Regression statistics table. | # Regression statistics table. | ||
# ANOVA table. | # ANOVA table. | ||
# Residual output. | # Residual output. | ||
| − | + | 1.'''Regression statistics''' : | |
| − | *It contains multiple R, R Square, Adjusted | + | *It contains multiple R, R Square, Adjusted R Square, Standard Error and observations. |
| − | *R square gives the | + | *R square gives the fitness of the data with the regression line. |
*That value is closer to 1 is the better the regression line fits the data. | *That value is closer to 1 is the better the regression line fits the data. | ||
*Standard Error refers to the estimated standard deviation of the error term. It is called the standard error of the regression. | *Standard Error refers to the estimated standard deviation of the error term. It is called the standard error of the regression. | ||
| − | + | 2.'''ANOVA table''': | |
*ANOVA is the analysis of variance. | *ANOVA is the analysis of variance. | ||
*This table splits in to two components which is Residual and Regression. | *This table splits in to two components which is Residual and Regression. | ||
| − | + | Total sum of squares = Residual (error) sum of squares + Regression (explained) sum of squares. | |
*Also this table gives the probability, T stat, significance of F and P. | *Also this table gives the probability, T stat, significance of F and P. | ||
*When the significance of F is < 0.05, then the result for the given data is statistically significant. | *When the significance of F is < 0.05, then the result for the given data is statistically significant. | ||
*When the significance of F is > 0.05, then better to stop using this set of independent variables. | *When the significance of F is > 0.05, then better to stop using this set of independent variables. | ||
| − | *Then remove a variable with a high P-value and | + | *Then remove a variable with a high P-value and return the regression until Significance F drops below 0.05. |
*So the Significance of P value should be <0.05. | *So the Significance of P value should be <0.05. | ||
*This table containing the regression coefficient values also. | *This table containing the regression coefficient values also. | ||
| − | + | 3.'''Residual output''': | |
| − | *The residuals show you how far away the actual data points are | + | *The residuals show you how far away the actual data points are from the predicted data points. |
| − | |||
==Examples== | ==Examples== | ||
| − | {| class="wikitable" | + | 1. |
| − | |+Spreadsheet | + | {| class="wikitable" |
| − | |- | + | |+Spreadsheet |
| − | ! !! A !! B | + | |- |
| − | |- | + | ! !! A !! B |
| − | ! 1 | + | |- |
| − | | '''Temperature''' || '''Drying Time(Hrs)''' | + | ! 1 |
| − | |- | + | | '''Temperature''' || '''Drying Time(Hrs)''' |
| − | ! 2 | + | |- |
| − | | 54 || 8 | + | ! 2 |
| − | |- | + | | 54 || 8 |
| − | ! 3 | + | |- |
| − | | 63 || 6 | + | ! 3 |
| − | |- | + | | 63 || 6 |
| − | ! 4 | + | |- |
| − | | 75 || 3 | + | ! 4 |
| − | |- | + | | 75 || 3 |
| − | ! 5 | + | |- |
| − | | 82 || 1 | + | ! 5 |
| − | |} | + | | 82 || 1 |
| + | |} | ||
=REGRESSIONANALYSIS(A2:A5,B2:B5) | =REGRESSIONANALYSIS(A2:A5,B2:B5) | ||
| + | '''REGRESSION ANALYSIS OUTPUT''' | ||
{| class="wikitable" | {| class="wikitable" | ||
|+Summary Output | |+Summary Output | ||
|- | |- | ||
| − | ! Regression !! | + | ! Regression Statistics !! |
|- | |- | ||
| Multiple R || -0.9989241524588298 | | Multiple R || -0.9989241524588298 | ||
| Line 91: | Line 95: | ||
| 86.5 || 0.6885767430246738 || 125.62143708199632|| 0.00006336233990811291 || 83.53729339698289 || 89.46270660301711 | | 86.5 || 0.6885767430246738 || 125.62143708199632|| 0.00006336233990811291 || 83.53729339698289 || 89.46270660301711 | ||
|- | |- | ||
| − | ! X | + | ! X Variable |
| − | | 1 || 2 || 0.5 || || | + | | -4 || 0.13130643285972046 || -30.463092423456118 || 0.0010758475411701829 || -4.564965981777541 || -3.435034018222459 |
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+Residual Output | ||
| + | |- | ||
| + | ! Observation !! Predicted Y !! Residuals !! Standard Residuals | ||
| + | |- | ||
| + | | 1 || 54.5 || -0.5 ||-0.8660254037844387 | ||
| + | |- | ||
| + | | 2 || 62.5 || 0.5 || 0.8660254037844387 | ||
| + | |- | ||
| + | | 3 || 74.5 || 0.5 || 0.8660254037844387 | ||
| + | |- | ||
| + | | 4 || 82.5 || -0.5 || -0.8660254037844387 | ||
| + | |} | ||
| + | |||
| + | 2. | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | '''Unit sales''' || ''' Ads ''' || ''' population''' | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 4000|| 12000 || 300000 | ||
| + | |- | ||
| + | ! 3 | ||
| + | | 5200 || 13150 || 411000 | ||
| + | |- | ||
| + | ! 4 | ||
| + | | 6800 || 14090 || 500000 | ||
| + | |- | ||
| + | ! 5 | ||
| + | | 8000 || 11900 || 650000 | ||
| + | |- | ||
| + | !6 | ||
| + | |10000 || 15000 || 800000 | ||
| + | |} | ||
| + | |||
| + | #REGRESSIONANALYSIS(A2:A6,B2:C6) | ||
| + | '''REGRESSION ANALYSIS OUTPUT''' | ||
| + | {| class="wikitable" | ||
| + | |+SUMMARY OUTPUT | ||
| + | |- | ||
| + | ! Regression Statistics !! | ||
| + | |- | ||
| + | ! Multiple R | ||
| + | | 0.9973790019059987 | ||
| + | |- | ||
| + | ! R Square | ||
| + | | 0.9947648734430062 | ||
| + | |- | ||
| + | ! Adjusted R Square | ||
| + | | 0.9895297468860125 | ||
| + | |- | ||
| + | ! Standard Error | ||
| + | | 240.4075647503864 | ||
| + | |- | ||
| + | ! Observations | ||
| + | | 5 | ||
| + | |} | ||
| + | {| class="wikitable" | ||
| + | |+ANOVA | ||
| + | |- | ||
| + | ! !! df !!SS !! MS !! F!! Significance F | ||
| + | |- | ||
| + | ! Regression: | ||
| + | | 2 || 21964408.405621577 || 10982204.202810789 || 190.0173496501376 || 0.00523512655699377 | ||
| + | |- | ||
| + | ! Residual: | ||
| + | | 2 ||115591.59437842245|| 57795.797189211225|| || | ||
| + | |- | ||
| + | ! Total: | ||
| + | | 4 || 22080000 || || || | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! !!Coefficients!! Standard Error !! t Stat !! P-value !! Lower 95%!! Upper 95% ||Lower 95.0% || Upper 95.0% | ||
| + | |- | ||
| + | ! Intercept: | ||
| + | | -1096.09242|| 1259.21057|| -0.87046|| 0.47583 || -6514.03824|| 4321.85339 || -6514.03824|| 4321.8533 | ||
| + | |- | ||
| + | ! X Variable1 | ||
| + | | 0.14076 ||0.10798|| 1.30359 || 0.32223|| -0.32384 || 0.60538 ||-0.32384 || 0.60538 | ||
| + | |- | ||
| + | !X Variable2 | ||
| + | | 0.01133 || 0.00073|| 15.45951 || 0.00415 || 0.00818 || 0.01449 || 0.00818 || 0.01449 | ||
| + | |} | ||
| + | {| class="wikitable" | ||
| + | |+Residual Output | ||
| + | |- | ||
| + | ! Observation !! Predicted Y !! Residuals !! Standard Residuals | ||
| + | |- | ||
| + | | 1 || 593.1069112686723 || 3406.8930887313277 || 1.5209125615152896 | ||
| + | |- | ||
| + | | 2 || 754.9885142857306 || 4445.011485714269 || 1.9843516155712606 | ||
| + | |- | ||
| + | | 3 || 887.3091289257611 || 5912.690871074239 || 2.6395562126436793 | ||
| + | |- | ||
| + | | 4 || 579.0302501367541 || 7420.969749863246 ||3.312885323147887 | ||
|- | |- | ||
| − | + | | 5 || 1015.4067452262161 || 8984.593254773783 ||4.010921501026477 | |
| − | | | ||
|} | |} | ||
| − | + | ==Related Videos== | |
| − | + | ||
| − | + | {{#ev:youtube|OlxiOJ26r_k|280|center|REGRESSION}} | |
| − | |||
| − | |||
| − | |||
| − | |||
==See Also== | ==See Also== | ||
| + | *[[Manuals/calci/SLOPE| SLOPE]] | ||
| + | *[[Manuals/calci/STEYX| STEYX]] | ||
==References== | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Regression_analysis Regression] | ||
Latest revision as of 06:02, 9 May 2016
REGRESSIONANALYSIS(y,x)
Regression analysis is a form of predictive modelling technique which investigates the relationship between a dependent (target) and independent variable (s) (predictor). This technique is used for forecasting, time series modelling and finding the causal effect relationship between the variables.
- is the set of dependent variables .
- is the set of independent variables.
Description
- This function is calculating the Regression analysis of the given data.
- This analysis is very useful for the analyzing the large amounts of data and making predictions.
- This analysis give the result in three table values.
- Regression statistics table.
- ANOVA table.
- Residual output.
1.Regression statistics :
- It contains multiple R, R Square, Adjusted R Square, Standard Error and observations.
- R square gives the fitness of the data with the regression line.
- That value is closer to 1 is the better the regression line fits the data.
- Standard Error refers to the estimated standard deviation of the error term. It is called the standard error of the regression.
2.ANOVA table:
- ANOVA is the analysis of variance.
- This table splits in to two components which is Residual and Regression.
Total sum of squares = Residual (error) sum of squares + Regression (explained) sum of squares.
- Also this table gives the probability, T stat, significance of F and P.
- When the significance of F is < 0.05, then the result for the given data is statistically significant.
- When the significance of F is > 0.05, then better to stop using this set of independent variables.
- Then remove a variable with a high P-value and return the regression until Significance F drops below 0.05.
- So the Significance of P value should be <0.05.
- This table containing the regression coefficient values also.
3.Residual output:
- The residuals show you how far away the actual data points are from the predicted data points.
Examples
1.
| A | B | |
|---|---|---|
| 1 | Temperature | Drying Time(Hrs) |
| 2 | 54 | 8 |
| 3 | 63 | 6 |
| 4 | 75 | 3 |
| 5 | 82 | 1 |
=REGRESSIONANALYSIS(A2:A5,B2:B5)
REGRESSION ANALYSIS OUTPUT
| Regression Statistics | |
|---|---|
| Multiple R | -0.9989241524588298 |
| R Square | 0.9978494623655915 |
| v14193 | 0.9967741935483871 |
| v15308 | 0.7071067811865362 |
| Source of Variation | Sum Of Squares | Degree Of Freedom | Mean Of Squares | F | Significance F |
|---|---|---|---|---|---|
| Regression: | 464 | 1 | 464 | 928 | 0.0010758475411702228 |
| Residual: | 1 | 2 | 0.5 | ||
| Total: | 465 | 3 |
| Coefficients | Standard Error | T Statistics | Probability | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intercept: | 86.5 | 0.6885767430246738 | 125.62143708199632 | 0.00006336233990811291 | 83.53729339698289 | 89.46270660301711 |
| X Variable | -4 | 0.13130643285972046 | -30.463092423456118 | 0.0010758475411701829 | -4.564965981777541 | -3.435034018222459 |
| Observation | Predicted Y | Residuals | Standard Residuals |
|---|---|---|---|
| 1 | 54.5 | -0.5 | -0.8660254037844387 |
| 2 | 62.5 | 0.5 | 0.8660254037844387 |
| 3 | 74.5 | 0.5 | 0.8660254037844387 |
| 4 | 82.5 | -0.5 | -0.8660254037844387 |
2.
| A | B | C | |
|---|---|---|---|
| 1 | Unit sales | Ads | population |
| 2 | 4000 | 12000 | 300000 |
| 3 | 5200 | 13150 | 411000 |
| 4 | 6800 | 14090 | 500000 |
| 5 | 8000 | 11900 | 650000 |
| 6 | 10000 | 15000 | 800000 |
- REGRESSIONANALYSIS(A2:A6,B2:C6)
REGRESSION ANALYSIS OUTPUT
| Regression Statistics | |
|---|---|
| Multiple R | 0.9973790019059987 |
| R Square | 0.9947648734430062 |
| Adjusted R Square | 0.9895297468860125 |
| Standard Error | 240.4075647503864 |
| Observations | 5 |
| df | SS | MS | F | Significance F | |
|---|---|---|---|---|---|
| Regression: | 2 | 21964408.405621577 | 10982204.202810789 | 190.0173496501376 | 0.00523512655699377 |
| Residual: | 2 | 115591.59437842245 | 57795.797189211225 | ||
| Total: | 4 | 22080000 |
| Coefficients | Standard Error | t Stat | P-value | Lower 95% | Upper 95% | Lower 95.0% | Upper 95.0% | |
|---|---|---|---|---|---|---|---|---|
| Intercept: | -1096.09242 | 1259.21057 | -0.87046 | 0.47583 | -6514.03824 | 4321.85339 | -6514.03824 | 4321.8533 |
| X Variable1 | 0.14076 | 0.10798 | 1.30359 | 0.32223 | -0.32384 | 0.60538 | -0.32384 | 0.60538 |
| X Variable2 | 0.01133 | 0.00073 | 15.45951 | 0.00415 | 0.00818 | 0.01449 | 0.00818 | 0.01449 |
| Observation | Predicted Y | Residuals | Standard Residuals |
|---|---|---|---|
| 1 | 593.1069112686723 | 3406.8930887313277 | 1.5209125615152896 |
| 2 | 754.9885142857306 | 4445.011485714269 | 1.9843516155712606 |
| 3 | 887.3091289257611 | 5912.690871074239 | 2.6395562126436793 |
| 4 | 579.0302501367541 | 7420.969749863246 | 3.312885323147887 |
| 5 | 1015.4067452262161 | 8984.593254773783 | 4.010921501026477 |
Related Videos
See Also
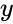 is the set of dependent variables .
is the set of dependent variables . is the set of independent variables.
is the set of independent variables.