Difference between revisions of "Manuals/calci/HARMONICSERIES"
| (7 intermediate revisions by 2 users not shown) | |||
| Line 6: | Line 6: | ||
==Description== | ==Description== | ||
*This sfunction displays the Harmonic series of the numbers. | *This sfunction displays the Harmonic series of the numbers. | ||
| − | *A series is an expression with an infinite number of terms, like this:<math>\sum_{n=1}^{ | + | *A series is an expression with an infinite number of terms, like this:<math>\sum_{n=1}^{\infty} \frac{1}{n} = 1+ \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....</math> |
*This is the divergent infinite series. | *This is the divergent infinite series. | ||
*In HARMONICSERIES(Start,Numbers,OnlyNth),Start is the beginning number of the series, Numbers is number of the number in the series and OnlyNth is the nth term of the Harmonic Series. | *In HARMONICSERIES(Start,Numbers,OnlyNth),Start is the beginning number of the series, Numbers is number of the number in the series and OnlyNth is the nth term of the Harmonic Series. | ||
*Every term of the series after the first is the harmonic mean of the neighboring terms. | *Every term of the series after the first is the harmonic mean of the neighboring terms. | ||
*The phrase harmonic mean likewise derives from music. | *The phrase harmonic mean likewise derives from music. | ||
| + | |||
| + | ==Examples== | ||
| + | #HARMONICSERIES(3,10,4) = 0.3333333333333333 | ||
| + | #HARMONICSERIES(189,20,18) = 9.947368421052632 | ||
| + | |||
| + | ==Related Videos== | ||
| + | {{#ev:youtube|v=OqBZCycIYfw|280|center|Harmonic Series}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/HARMEAN| HARMEAN]] | ||
| + | *[[Manuals/calci/SUM | SUM ]] | ||
| + | |||
| + | ==References== | ||
| + | [https://en.wikipedia.org/wiki/Harmonic_series_(mathematics) Harmonic series] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:40, 28 November 2018
HARMONICSERIES (Start,Numbers,OnlyNth)
- are any positive integer .
- is the number of the series.
- is the Nth term of the series.
Description
- This sfunction displays the Harmonic series of the numbers.
- A series is an expression with an infinite number of terms, like this:
- This is the divergent infinite series.
- In HARMONICSERIES(Start,Numbers,OnlyNth),Start is the beginning number of the series, Numbers is number of the number in the series and OnlyNth is the nth term of the Harmonic Series.
- Every term of the series after the first is the harmonic mean of the neighboring terms.
- The phrase harmonic mean likewise derives from music.
Examples
- HARMONICSERIES(3,10,4) = 0.3333333333333333
- HARMONICSERIES(189,20,18) = 9.947368421052632
Related Videos
See Also
References
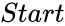 are any positive integer .
are any positive integer .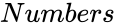 is the number of the series.
is the number of the series.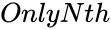 is the Nth term of the series.
is the Nth term of the series.