Difference between revisions of "Manuals/calci/PMT"
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''PMT( | + | <div style="font-size:30px">'''PMT (Rate,NoPaymentPeriods,PresentValue,FutureValue,Type)'''</div><br/> |
| − | *<math> | + | |
| − | *<math> | + | *<math>Rate </math> is the interest rate. |
| − | *<math> | + | *<math> NoPaymentPeriods </math> is the total number of payment periods. |
| − | *<math> | + | *<math> PresentValue </math> is the at present value. |
| − | *<math> | + | *<math> FutureValue</math> is the future value. |
| + | *<math> Type</math> is the type. | ||
| + | **PMT(), returns the periodic payment for an annuity | ||
| + | |||
==Description== | ==Description== | ||
*This functon gives the payment amount for the loan. | *This functon gives the payment amount for the loan. | ||
*It is based on the period, fixed payments and a fixed interest rate. | *It is based on the period, fixed payments and a fixed interest rate. | ||
| − | *In <math>PMT( | + | *In <math>PMT (Rate,NoPaymentPeriods,PresentValue,FutureValue,Type)</math> ,<math> Rate </math> is the annual rate of interest for the loan. |
| − | *Suppose we are taking a loan for 8 percent annual interest rate and paying the amount in monthly, then the <math> | + | *Suppose we are taking a loan for 8 percent annual interest rate and paying the amount in monthly, then the <math> Rate </math> value is 8%/12. |
| − | *So we have to enter the <math> | + | *So we have to enter the <math> Rate </math> value as 8%/12 or 0.6667% or 0.006667 in to the formula as the rate. |
| − | *<math> | + | *<math> NoPaymentPeriods </math> is the total number of payment periods in an annuity. |
| − | *<math> | + | *<math> PresentValue </math> is the present value or the amount borrowed or the principal of the loan. |
| − | *<math> | + | *<math> FutureValue </math> is the future value of an investment or loan (the value you want to achieve at the end of all periods) when we are omitting the value of <math>FutureValue </math> ,then it is assumed to be 0. |
*i.e.,future value of a loan is 0. | *i.e.,future value of a loan is 0. | ||
| − | *<math> | + | *<math> Type </math> is the number 0 or 1 which is specifies the time to make a payment during the period. |
| − | *when we are not giving the value of <math> | + | *when we are not giving the value of <math>Type</math>, then it is assumed to be 0. |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | ! | + | ! Type value |
! Explanation | ! Explanation | ||
|- | |- | ||
| Line 31: | Line 34: | ||
*The amount given by the function <math> PMT </math> not containing any taxes,rserve payments or extra fees related with the loan. | *The amount given by the function <math> PMT </math> not containing any taxes,rserve payments or extra fees related with the loan. | ||
*But it contains only the principal amount and interest only. | *But it contains only the principal amount and interest only. | ||
| − | *Also to calculate the total amount paid during the loan period, multiply the returned <math> PMT </math> value by <math> | + | *Also to calculate the total amount paid during the loan period, multiply the returned <math> PMT </math> value by <math> NoPaymentPeriods </math>. |
==ZOS Section== | ==ZOS Section== | ||
Latest revision as of 18:31, 23 July 2018
PMT (Rate,NoPaymentPeriods,PresentValue,FutureValue,Type)
- is the interest rate.
- is the total number of payment periods.
- is the at present value.
- is the future value.
- is the type.
- PMT(), returns the periodic payment for an annuity
Description
- This functon gives the payment amount for the loan.
- It is based on the period, fixed payments and a fixed interest rate.
- In , is the annual rate of interest for the loan.
- Suppose we are taking a loan for 8 percent annual interest rate and paying the amount in monthly, then the value is 8%/12.
- So we have to enter the value as 8%/12 or 0.6667% or 0.006667 in to the formula as the rate.
- is the total number of payment periods in an annuity.
- is the present value or the amount borrowed or the principal of the loan.
- is the future value of an investment or loan (the value you want to achieve at the end of all periods) when we are omitting the value of ,then it is assumed to be 0.
- i.e.,future value of a loan is 0.
- is the number 0 or 1 which is specifies the time to make a payment during the period.
- when we are not giving the value of , then it is assumed to be 0.
| Type value | Explanation |
|---|---|
| 0 | Payments are due at the end of the period |
| 1 | Payments are due at the beginning of the period |
- The amount given by the function not containing any taxes,rserve payments or extra fees related with the loan.
- But it contains only the principal amount and interest only.
- Also to calculate the total amount paid during the loan period, multiply the returned value by .
ZOS Section
- The function to calculate PMT in ZOS is PMT(Rate,NoPaymentPeriods,PresentValue,FutureValue,Type)
- is the interest rate.
- is the total number of payment periods.
- is the current value for the amount.
- is the future value.
- For e.g.,PMT(0.62/12,19..22,34000)
Examples
- =PMT(0.11/12,14,25000) = -1910.908677870
- =PMT(0.09/12,20,50000,10000,0) = -3166.8379163721
- =PMT(0.09/12,20,50000,10000,1) = -3143.26344056
Related Videos
See Also
References
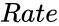 is the interest rate.
is the interest rate. is the total number of payment periods.
is the total number of payment periods.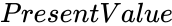 is the at present value.
is the at present value.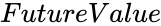 is the future value.
is the future value.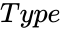 is the type.
is the type.