Difference between revisions of "Manuals/calci/SQRT"
Jump to navigation
Jump to search
| (16 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''SQRT(Value)'''</div><br/> |
| + | *<math>Value</math> is any positive number. | ||
| + | **SQRT(), returns a positive square root. | ||
| − | + | ==Description== | |
| − | + | *This function gives the square root of a positive real number. | |
| − | + | *Squaring is the value that can be multiplied by itself to give the original number. | |
| − | + | *The square root of a number is the inverse operation of squaring that number. | |
| − | + | *The root of a number is an equal factor of the number. | |
| − | + | *Every non-negative real number a has only one non-negative square root, called the principal square root, which is denoted by <math>\sqrt{a}</math>, where <math>\sqrt{}</math> is called the radical sign or radix. | |
| − | + | *Square roots of positive whole numbers that are not perfect squares are always irrational numbers. | |
| − | + | *Numbers not expressible as a ratio of two integers . | |
| − | + | This function will give the result as NaN when n is a negative number. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | < | ||
| − | |||
| − | { | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Examples== | ||
| + | #=SQRT(0)=0 | ||
| + | #=SQRT(1)=1 | ||
| + | #=SQRT(136)= 11.661903789690601 | ||
| + | #=SQRT(ABS(-625))= 25 | ||
| + | #=1..10@SQRT | ||
{| class="wikitable" | {| class="wikitable" | ||
| + | |+1..10@SQRT | ||
|- | |- | ||
| − | ! Number !! | + | ! Number !! Square Root |
|- | |- | ||
| 1 || 1 | | 1 || 1 | ||
|- | |- | ||
| − | | 2 || 1.4142135623730951 | + | | 2 || 1.4142135623730951 |
|- | |- | ||
| − | | 3 || 1.7320508075688772 | + | |3 || 1.7320508075688772 |
|- | |- | ||
| − | | 4 || 2 | + | |4 || 2 |
|- | |- | ||
| 5 || 2.23606797749979 | | 5 || 2.23606797749979 | ||
| Line 96: | Line 43: | ||
|- | |- | ||
| 10 || 3.1622776601683795 | | 10 || 3.1622776601683795 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|ROIfbUQrSY4|280|center|SQRT}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/SQRTPI | SQRTPI ]] | ||
| + | *[[Manuals/calci/POWER | POWER ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Square_root Square Root] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:20, 22 April 2019
SQRT(Value)
- is any positive number.
- SQRT(), returns a positive square root.
Description
- This function gives the square root of a positive real number.
- Squaring is the value that can be multiplied by itself to give the original number.
- The square root of a number is the inverse operation of squaring that number.
- The root of a number is an equal factor of the number.
- Every non-negative real number a has only one non-negative square root, called the principal square root, which is denoted by , where is called the radical sign or radix.
- Square roots of positive whole numbers that are not perfect squares are always irrational numbers.
- Numbers not expressible as a ratio of two integers .
This function will give the result as NaN when n is a negative number.
Examples
- =SQRT(0)=0
- =SQRT(1)=1
- =SQRT(136)= 11.661903789690601
- =SQRT(ABS(-625))= 25
- =1..10@SQRT
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.4142135623730951 |
| 3 | 1.7320508075688772 |
| 4 | 2 |
| 5 | 2.23606797749979 |
| 6 | 2.449489742783178 |
| 7 | 2.6457513110645907 |
| 8 | 2.8284271247461903 |
| 9 | 3 |
| 10 | 3.1622776601683795 |
Related Videos
See Also
References
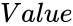 is any positive number.
is any positive number.
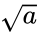 , where
, where 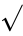 is called the radical sign or radix.
is called the radical sign or radix.