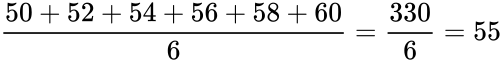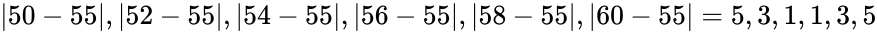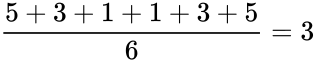Difference between revisions of "Manuals/calci/AVEDEV"
Jump to navigation
Jump to search
| (43 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''AVEDEV( | + | <div style="font-size:30px">'''AVEDEV()'''</div><br/> |
| − | * | + | *Parameters are any set of any real numbers. |
| + | **AVEDEV(),returns the average of the absolute deviations of data points from their mean. | ||
==Description== | ==Description== | ||
| − | * | + | |
| − | *Arguments can be numbers, names, arrays | + | *This function is used to find the average of the absolute deviations of data points from its mean. |
| + | *Arguments can be numbers,names,arrays or references. | ||
This function gives the average absolute deviation of a given set of numbers. | This function gives the average absolute deviation of a given set of numbers. | ||
The Average deviation is calculated in three steps: | The Average deviation is calculated in three steps: | ||
#We have to find the mean <math>\bar{x}</math>. | #We have to find the mean <math>\bar{x}</math>. | ||
#To find the deviation of each value, subtract all numbers with its mean value. | #To find the deviation of each value, subtract all numbers with its mean value. | ||
| − | #Then find the average deviation, add all the deviation values and divide by the number of given | + | #Then find the average deviation, add all the deviation values and divide by the total number of given numbers. |
| − | + | :<math>Average Deviation =\sum_{i=1}^{n} \frac{x_i-\bar{x}}{n}</math> | |
| − | <math>Average Deviation =\sum_{i=1}^n \frac{ | + | *Here <math>x_i</math> is the observation. |
| − | |||
| − | *Here <math> | ||
*<math>\bar{x}</math> is the mean. | *<math>\bar{x}</math> is the mean. | ||
*<math>n</math> is the number of given set of observations. | *<math>n</math> is the number of given set of observations. | ||
Here we have to give more than one arguments. Arguments can be either number, name,logical values, arrays or cell references that contain numbers. | Here we have to give more than one arguments. Arguments can be either number, name,logical values, arrays or cell references that contain numbers. | ||
This function will give the result as error, when the text couldn't convert in to numbers. | This function will give the result as error, when the text couldn't convert in to numbers. | ||
| + | |||
| + | |||
| + | ==ZOS== | ||
| + | |||
| + | *The syntax is to calculate AVEDEV in ZOS is <math>AVEDEV()</math>. | ||
| + | **Parameters are any set of any real numbers. | ||
| + | *For e.g.,AVEDEV(-25..-12) | ||
| + | {{#ev:youtube|_hYy71RCZxg|280|center|AVEDEV}} | ||
==Examples== | ==Examples== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *=AVEDEV(50,52, 54, 56, 58, 60) gives the result 3<br/> | |
| − | =AVEDEV (B2:B5) | + | '''Steps''' |
| + | #Mean = <math>\frac{50+52+ 54+ 56+ 58+ 60}{6} = \frac{330}{6} = 55</math> | ||
| + | #Deviation =<math> |50-55|,|52-55|,|54-55|,|56-55|,|58-55|,|60-55| = 5,3,1,1,3,5</math> | ||
| + | #Average Deviation = <math>\frac{5+3+1+1+3+5}{6} = 3</math> | ||
| + | *=AVEDEV(-20,40,-30,50,60) = 36 | ||
| + | *=AVEDEV(-1.2,3.5,7,2,8.3,9.1) = 3.35 | ||
| + | *=AVEDEV(B2:B5) = 1.75 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|GdIkEngwGNU|280|center|Mean Absolute Deviation}} | ||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | *[[Manuals/calci/SUM | SUM]] | ||
| + | *[[Manuals/calci/AVERAGE | AVERAGE ]] | ||
| + | *[[Manuals/calci/AVERAGEA | AVERAGEA ]] | ||
| + | |||
| + | |||
| + | ==References== | ||
| + | |||
| + | [http://en.wikipedia.org/wiki/Absolute_deviation Average Deviation] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 01:34, 11 August 2020
AVEDEV()
- Parameters are any set of any real numbers.
- AVEDEV(),returns the average of the absolute deviations of data points from their mean.
Description
- This function is used to find the average of the absolute deviations of data points from its mean.
- Arguments can be numbers,names,arrays or references.
This function gives the average absolute deviation of a given set of numbers. The Average deviation is calculated in three steps:
- We have to find the mean .
- To find the deviation of each value, subtract all numbers with its mean value.
- Then find the average deviation, add all the deviation values and divide by the total number of given numbers.
- Here is the observation.
- is the mean.
- is the number of given set of observations.
Here we have to give more than one arguments. Arguments can be either number, name,logical values, arrays or cell references that contain numbers.
This function will give the result as error, when the text couldn't convert in to numbers.
ZOS
- The syntax is to calculate AVEDEV in ZOS is .
- Parameters are any set of any real numbers.
- For e.g.,AVEDEV(-25..-12)
Examples
- =AVEDEV(50,52, 54, 56, 58, 60) gives the result 3
Steps
- Mean =
- Deviation =
- Average Deviation =
- =AVEDEV(-20,40,-30,50,60) = 36
- =AVEDEV(-1.2,3.5,7,2,8.3,9.1) = 3.35
- =AVEDEV(B2:B5) = 1.75
Related Videos
See Also
References
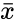 .
.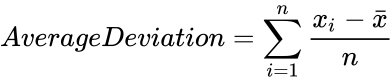
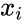 is the observation.
is the observation. is the number of given set of observations.
is the number of given set of observations.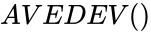 .
.