Difference between revisions of "Manuals/calci/EXP"
Jump to navigation
Jump to search
| (18 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''EXP(x)'''</div><br/> | <div style="font-size:30px">'''EXP(x)'''</div><br/> | ||
*where <math>x</math> is the number . | *where <math>x</math> is the number . | ||
| + | |||
| + | *EXP() returns e raised to the power of a given number | ||
| + | |||
==Description== | ==Description== | ||
*This function gives the <math>e</math> raised to the power of number. | *This function gives the <math>e</math> raised to the power of number. | ||
| − | *In <math>EXP(x)</math>, where <math>x</math> represents the exponent of <math>e</math> | + | *In <math>EXP(x)</math>, where <math>x</math> represents the exponent of <math>e</math> or <math>e^x</math>. |
| − | *The approximate value of the constant <math>e=2.718281828459045<math> and it is equal to <math>e^x</math> or <math>EXP(1)<math>. | + | *The approximate value of the constant <math>e=2.718281828459045</math> and it is equal to <math>e^x</math> or <math>EXP(1)</math>. |
*It is called the Mathematical Constant or Euler's Number or Napier's Constant. | *It is called the Mathematical Constant or Euler's Number or Napier's Constant. | ||
*It is the base of natural logarithm. | *It is the base of natural logarithm. | ||
| − | *It can calculate the sum of infinite series: <math>e=1+ | + | *It can be calculate the sum of infinite series: <math>e=1+\frac{1}{1}+\frac{1}{1.2}+\frac{1}{1.2.3}+\frac{1}{1.2.3.4} +...</math> |
*And the inverse function of the natural logarithm function is the exponential function: | *And the inverse function of the natural logarithm function is the exponential function: | ||
| − | + | <math>f^{-1}(x) = e^x</math>. | |
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate the EXP in ZOS is <math>EXP(x)</math>. | ||
| + | **where <math>x</math> is the number . | ||
| + | *For e.g.,(-9)..5..2@EXP | ||
| + | {{#ev:youtube|k1aWYvtxxrI|280|center|Exponential}} | ||
==Examples== | ==Examples== | ||
| − | *EXP(1)=2.718281828459045 | + | *=EXP(1)=2.718281828459045 |
| − | *EXP(0)=1 | + | *=EXP(0)=1 |
| − | *EXP(-5)=0.0067379469990 | + | *=EXP(-5)=0.0067379469990 |
| − | *EXP(6.3)=544.5719101259 | + | *=EXP(6.3)=544.5719101259 |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=T3zzvj6wSCQ|280|center|EXP Function}} | ||
==See Also== | ==See Also== | ||
| + | |||
*[[Manuals/calci/IMEXP | IMEXP ]] | *[[Manuals/calci/IMEXP | IMEXP ]] | ||
*[[Manuals/calci/LOG | LOG ]] | *[[Manuals/calci/LOG | LOG ]] | ||
| Line 24: | Line 38: | ||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/ | + | [http://en.wikipedia.org/wiki/Exponential_function Exponential function] |
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:21, 19 November 2018
EXP(x)
- where is the number .
- EXP() returns e raised to the power of a given number
Description
- This function gives the raised to the power of number.
- In , where represents the exponent of or .
- The approximate value of the constant and it is equal to or .
- It is called the Mathematical Constant or Euler's Number or Napier's Constant.
- It is the base of natural logarithm.
- It can be calculate the sum of infinite series:
- And the inverse function of the natural logarithm function is the exponential function:
.
ZOS
- The syntax is to calculate the EXP in ZOS is .
- where is the number .
- For e.g.,(-9)..5..2@EXP
Examples
- =EXP(1)=2.718281828459045
- =EXP(0)=1
- =EXP(-5)=0.0067379469990
- =EXP(6.3)=544.5719101259
Related Videos
See Also
References
 is the number .
is the number .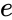 raised to the power of number.
raised to the power of number.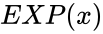 , where
, where 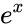 .
.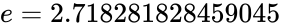 and it is equal to
and it is equal to 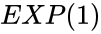 .
.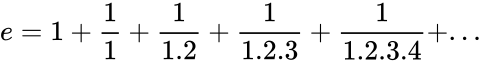
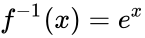 .
.