Difference between revisions of "Manuals/calci/BETAINV"
Jump to navigation
Jump to search
| (21 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size: | + | <div style="font-size:25px">'''BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)'''</div><br/> |
| − | * | + | *<math>Probability</math> is the probability value associated with the beta distribution. |
| − | *Alpha& | + | *<math>Alpha</math> & <math>Beta</math> are the values of the shape parameter. |
| − | * | + | *<math>LowerBound</math> & <math>UpperBound</math> the lower and upper limit to the interval of <math>x</math>. |
| + | *<math>Accuracy</math> gives accurate value of the solution. | ||
| + | *<math>DivisionsAndDepthArray</math> is the value of the division. | ||
| + | **BETAINV(), returns the inverse of the Cumulative Distribution Function for a specified beta distribution. | ||
| + | |||
==Description== | ==Description== | ||
| − | *This function gives the inverse value of | + | *This function gives the inverse value of Cumulative Beta Probability Distribution. |
| − | *It is called | + | *It is called Inverted Beta Function or Beta Prime. |
| − | *In BETAINV( | + | *In <math>BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)</math>, <math>Probability</math> is the probability value associated with Beta Distribution, <math>Alpha</math> and <math>Beta</math> are the values of two positive shape parameters and <math>LowerBound</math> and <math>UpperBound</math> are the lower and upper limit. |
| − | *If BETADIST( | + | *Normally the limit values are optional, i.e. when we are giving the values of <math>LowerBound</math>&<math>UpperBound</math> then the result value is from <math>a</math> and <math>b</math>. |
| − | *BETAINV | + | *When we are omitting the values <math>LowerBound</math> and <math>UpperBound</math>, by default it will consider <math>LowerBound=0</math> and <math>UpperBound=1</math>, so the result value is from <math>0</math> and <math>1</math>. |
| + | *If <math>BETADIST (Number,Alpha,Beta,LowerBound,UpperBound)=Probability</math>, then <math>BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)=x</math>. | ||
| + | *<math>BETAINV</math> use the iterating method to find the value of <math>x</math>.suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
*This function will give the error result when | *This function will give the error result when | ||
| − | + | 1.Any one of the arguments are non-numeric | |
| − | + | 2.Alpha or Beta <math>\le</math> 0 | |
| − | + | 3.Number<LowerBound ,Number>UpperBound or LowerBound = UpperBound | |
| − | + | 4.we are not mentioning the limit values for LowerBound & UpperBound , | |
| + | by default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1 | ||
| + | |||
| + | ==ZOS== | ||
| + | |||
| + | *The syntax is to calculate of this function in ZOS is <math>BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)</math>. | ||
| + | **<math>probability</math> is the probability value associated with the beta distribution. | ||
| + | **<math>Alpha</math> and <math>Beta</math> are the values of the shape parameter. | ||
| + | **For e.g.,BETAINV(0.30987,10,18,12,16) | ||
| + | |||
==Examples== | ==Examples== | ||
| − | #BETAINV(0.2060381025,5,9,2,6)=3 | + | #BETAINV(0.2060381025,5,9,2,6) = 3 |
| − | #BETAINV(0.359492343,8,10) | + | #BETAINV(0.359492343,8,10) = 1.75 |
| − | + | #BETAINV(0.685470581,5,8,2,6) = 3.75 | |
| − | #BETAINV(0.685470581,5,8,2,6 | + | #BETAINV(0.75267,1,7,7,9) = 7.25 |
| − | + | #BETAINV(0.5689,-2,4,3,5) = #N/A (ALPHA GREATER THAN (OR) NOT EQUAL TO 0) | |
| − | #BETAINV(0.75267,1,7,7,9 | + | |
| − | + | ==Related Videos== | |
| − | #BETAINV(0.5689,-2,4,3,5)= | + | |
| + | {{#ev:youtube|v=KjlIoium8n4|280|center|Beta Inverse Distribution}} | ||
==See Also== | ==See Also== | ||
| Line 30: | Line 46: | ||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/Beta_distribution Beta Distribution] | + | [http://en.wikipedia.org/wiki/Beta_distribution Beta Distribution] |
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 03:50, 24 August 2020
BETAINV (Probability,Alpha,Beta,LowerBound,UpperBound,Accuracy,DivisionsAndDepthArray)
- is the probability value associated with the beta distribution.
- & are the values of the shape parameter.
- & the lower and upper limit to the interval of .
- gives accurate value of the solution.
- is the value of the division.
- BETAINV(), returns the inverse of the Cumulative Distribution Function for a specified beta distribution.
Description
- This function gives the inverse value of Cumulative Beta Probability Distribution.
- It is called Inverted Beta Function or Beta Prime.
- In , is the probability value associated with Beta Distribution, and are the values of two positive shape parameters and and are the lower and upper limit.
- Normally the limit values are optional, i.e. when we are giving the values of & then the result value is from and .
- When we are omitting the values and , by default it will consider and , so the result value is from and .
- If , then .
- use the iterating method to find the value of .suppose the iteration has not converged after 100 searches, then the function gives the error result.
- This function will give the error result when
1.Any one of the arguments are non-numeric 2.Alpha or Beta 0 3.Number<LowerBound ,Number>UpperBound or LowerBound = UpperBound 4.we are not mentioning the limit values for LowerBound & UpperBound , by default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1
ZOS
- The syntax is to calculate of this function in ZOS is .
- is the probability value associated with the beta distribution.
- and are the values of the shape parameter.
- For e.g.,BETAINV(0.30987,10,18,12,16)
Examples
- BETAINV(0.2060381025,5,9,2,6) = 3
- BETAINV(0.359492343,8,10) = 1.75
- BETAINV(0.685470581,5,8,2,6) = 3.75
- BETAINV(0.75267,1,7,7,9) = 7.25
- BETAINV(0.5689,-2,4,3,5) = #N/A (ALPHA GREATER THAN (OR) NOT EQUAL TO 0)
Related Videos
See Also
References
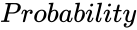 is the probability value associated with the beta distribution.
is the probability value associated with the beta distribution.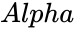 &
& 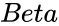 are the values of the shape parameter.
are the values of the shape parameter. &
& 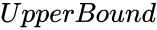 the lower and upper limit to the interval of
the lower and upper limit to the interval of  .
.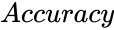 gives accurate value of the solution.
gives accurate value of the solution.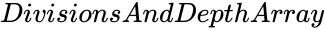 is the value of the division.
is the value of the division.
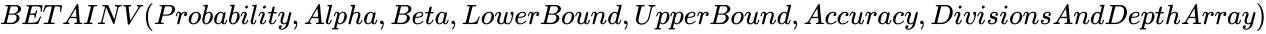 ,
,  and
and 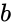 .
.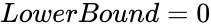 and
and 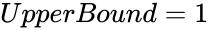 , so the result value is from
, so the result value is from 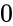 and
and  .
.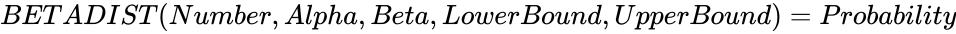 , then
, then 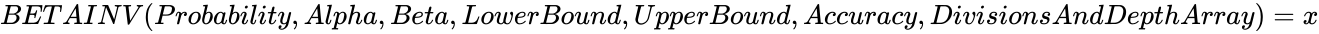 .
. use the iterating method to find the value of
use the iterating method to find the value of 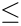 0
3.Number<LowerBound ,Number>UpperBound or LowerBound = UpperBound
4.we are not mentioning the limit values for LowerBound & UpperBound ,
by default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1
0
3.Number<LowerBound ,Number>UpperBound or LowerBound = UpperBound
4.we are not mentioning the limit values for LowerBound & UpperBound ,
by default it will consider the Standard Cumulative Beta Distribution, LowerBound = 0 and UpperBound = 1
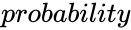 is the probability value associated with the beta distribution.
is the probability value associated with the beta distribution.