Difference between revisions of "Manuals/calci/FISHERINV"
Jump to navigation
Jump to search
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''FISHERINV( | + | <div style="font-size:30px">'''FISHERINV(Number)'''</div><br/> |
| − | *<math> | + | *<math>Number</math> is the value to find inverse of fisher transformation. |
| + | **FISHERINV(), returns the inverse of the Fisher transformation. | ||
| + | |||
==Description== | ==Description== | ||
*This function gives the inverse of the Fisher transformation. | *This function gives the inverse of the Fisher transformation. | ||
*We use this to test the correlations between set of data. | *We use this to test the correlations between set of data. | ||
| − | *The Inverse of the Fisher transformation is: <math>x= \frac {e^{2y-1}}{e^{2y+1}} i.e | + | *The Inverse of the Fisher transformation is: <math>x= \frac {e^{2y-1}}{e^{2y+1}}</math> i.e <math>y=FISHER(x)</math>, then <math>FISHERINV(y)=x</math> |
*It can be used to construct a confidence interval. | *It can be used to construct a confidence interval. | ||
| − | A confidence interval (CI) is a type of interval estimate of a population parameter and is used to indicate the reliability of an estimate. | + | *A confidence interval (CI) is a type of interval estimate of a population parameter and is used to indicate the reliability of an estimate. |
| − | + | This function will give the result as error when the <math>Number</math> value is non-numeric. | |
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate FISHERINV in ZOS is <math>FISHERINV(Number)</math>. | ||
| + | **<math>Number</math> is the value to find inverse of fisher transformation. | ||
| + | *For e.g.,FISHERINV(0.4521..0.507..0.01) | ||
| + | {{#ev:youtube|eGv4DvXyLhc|280|center|Inverse Fisher transformation}} | ||
==Examples== | ==Examples== | ||
| − | #FISHERINV(0.6389731838)=0.56419999998 | + | #FISHERINV(0.6389731838) = 0.56419999998 |
| − | #FISHERINV(0)=0 | + | #FISHERINV(0) = 0 |
| − | #FISHERINV(0.1234)=0.1227774315035342 | + | #FISHERINV(0.1234) = 0.1227774315035342 |
| − | #FISHERINV(1)=0.761594155955765 | + | #FISHERINV(1) = 0.761594155955765 |
| − | #FISHERINV(-0.4296)=-0.4049869686465480 | + | #FISHERINV(-0.4296) = -0.4049869686465480 |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|I0SjHVOHztc|280|center|Sampling Distributions}} | ||
==See Also== | ==See Also== | ||
| Line 21: | Line 33: | ||
*[[Manuals/calci/FISHER | FISHER ]] | *[[Manuals/calci/FISHER | FISHER ]] | ||
| + | ==References== | ||
| + | [http://en.wikipedia.org/wiki/F-distribution Fisher Distribution] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| − | + | *[[ Z3 | Z3 home ]] | |
| − | [ | ||
Latest revision as of 16:01, 7 August 2018
FISHERINV(Number)
- is the value to find inverse of fisher transformation.
- FISHERINV(), returns the inverse of the Fisher transformation.
Description
- This function gives the inverse of the Fisher transformation.
- We use this to test the correlations between set of data.
- The Inverse of the Fisher transformation is: i.e , then
- It can be used to construct a confidence interval.
- A confidence interval (CI) is a type of interval estimate of a population parameter and is used to indicate the reliability of an estimate.
This function will give the result as error when the value is non-numeric.
ZOS
- The syntax is to calculate FISHERINV in ZOS is .
- is the value to find inverse of fisher transformation.
- For e.g.,FISHERINV(0.4521..0.507..0.01)
Examples
- FISHERINV(0.6389731838) = 0.56419999998
- FISHERINV(0) = 0
- FISHERINV(0.1234) = 0.1227774315035342
- FISHERINV(1) = 0.761594155955765
- FISHERINV(-0.4296) = -0.4049869686465480
Related Videos
See Also
References
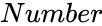 is the value to find inverse of fisher transformation.
is the value to find inverse of fisher transformation.
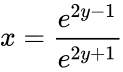 i.e
i.e 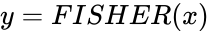 , then
, then 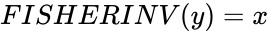
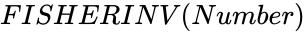 .
.