Difference between revisions of "Manuals/calci/FORECAST"
Jump to navigation
Jump to search
| (13 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''FORECAST( | + | <div style="font-size:30px">'''FORECAST (x,KnownYs,KnownXs) '''</div><br/> |
| − | *<math> | + | *<math>x</math> is the data point . |
| − | *<math> | + | *<math>KnownYs</math> is the dependent array of data. |
| − | *<math> | + | *<math>KnownXs</math> is the independent array of data. |
| − | + | **FORECAST(), returns a value along a linear trend. | |
==Description== | ==Description== | ||
| − | *This function gives the predicted value of the dependent variable for the specific value | + | *This function gives the predicted value of the dependent variable for the specific value <math>x</math>, of the independent variable by using a least squares linear regression to predict <math>y</math> values from <math>x</math> values. |
| − | *In <math>FORECAST( | + | *In <math>FORECAST (x,KnownYs,KnownXs)</math>, <math>x</math> is the data point to predict a value. |
| − | *The formula for <math>FORECAST</math> is <math> a+bx</math> | + | *<math>KnownYs</math> is the dependent array of data to predict the <math>y</math>-value and <math>KnownXs</math> is the independent array of data to predict the <math>y</math>-value. |
| + | *The formula for <math>FORECAST</math> is <math>a+bx</math> | ||
*where <math>a=\bar{y}-b \bar{x}</math> and <math> b=\frac{\sum (x-\bar{x})(y-\bar{y})}{\sum(x-\bar{x})^2}</math>. | *where <math>a=\bar{y}-b \bar{x}</math> and <math> b=\frac{\sum (x-\bar{x})(y-\bar{y})}{\sum(x-\bar{x})^2}</math>. | ||
| − | *Here <math>\bar{x}</math> and <math>\bar{y}</math> are the sample means of x and y. | + | *Here <math>\bar{x}</math> and <math>\bar{y}</math> are the sample means of <math>x</math> and <math>y</math>. |
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1. Any one of the value is | + | 1. Any one of the value is non-numeric. |
| − | 2. The values of | + | 2. The values of <math>KnownXs</math> and <math>KnownYs</math> are empty or contain a different number of data points. |
| − | 3. The variance of x is zero. | + | 3. The variance of <math>x</math> is zero. |
| + | ==ZOS== | ||
| + | |||
| + | *The syntax is to calculate this function in ZOS is <math>FORECAST (x, KnownYs, KnownXs)</math> | ||
| + | **<math>x</math> is the data points. | ||
| + | *For e.g.,FORECAST(30,[10,12,16,21,35],[9,14,23,39,76]) | ||
| + | *FORECAST(61,[22..28],[43..49]) | ||
==Examples== | ==Examples== | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
|+Spreadsheet | |+Spreadsheet | ||
| Line 48: | Line 44: | ||
|- | |- | ||
! 5 | ! 5 | ||
| − | | 32 || 41 || | + | | 32 || 41 || 2 || 5|| 9 ||17 |
|- | |- | ||
! 6 | ! 6 | ||
| − | | 4 || 10 || | + | | 4 || 10 || 4 || 14 || 28 |
|} | |} | ||
# =FORECAST(26,A1:A6,B1:B6) = 13.16666667 | # =FORECAST(26,A1:A6,B1:B6) = 13.16666667 | ||
# =FORECAST(18,C1:C4,D1:D4) = 2.119541779 | # =FORECAST(18,C1:C4,D1:D4) = 2.119541779 | ||
| + | # =FORECAST(24,E1:E4,F1:F4) = 31.71054889 | ||
| + | # =FORECAST(10,C5:F5,C6:E6) = NAN. | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|ksCVXXh5_hk|280|center|FORECAST}} | ||
==See Also== | ==See Also== | ||
| Line 60: | Line 62: | ||
*[[Manuals/calci/LINEST | LINEST]] | *[[Manuals/calci/LINEST | LINEST]] | ||
*[[Manuals/calci/LOGEST| LOGEST ]] | *[[Manuals/calci/LOGEST| LOGEST ]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://support.microsoft.com/en-us/kb/828236 FORECAST ] | ||
| − | + | ||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:07, 10 August 2018
FORECAST (x,KnownYs,KnownXs)
- is the data point .
- is the dependent array of data.
- is the independent array of data.
- FORECAST(), returns a value along a linear trend.
Description
- This function gives the predicted value of the dependent variable for the specific value , of the independent variable by using a least squares linear regression to predict values from values.
- In , is the data point to predict a value.
- is the dependent array of data to predict the -value and is the independent array of data to predict the -value.
- The formula for is
- where and .
- Here and are the sample means of and .
- This function will give the result as error when
1. Any one of the value is non-numeric. 2. The values of and are empty or contain a different number of data points. 3. The variance of is zero.
ZOS
- The syntax is to calculate this function in ZOS is
- is the data points.
- For e.g.,FORECAST(30,[10,12,16,21,35],[9,14,23,39,76])
- FORECAST(61,[22..28],[43..49])
Examples
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 5 | 30 | -28 | -42 | 51 | 46 |
| 2 | 9 | 32 | -18 | 34 | 14 | -1 |
| 3 | 11 | 15 | 35 | -13 | 0 | 29 |
| 4 | 18 | 28 | 12 | 25 | 60 | 18 |
| 5 | 32 | 41 | 2 | 5 | 9 | 17 |
| 6 | 4 | 10 | 4 | 14 | 28 |
- =FORECAST(26,A1:A6,B1:B6) = 13.16666667
- =FORECAST(18,C1:C4,D1:D4) = 2.119541779
- =FORECAST(24,E1:E4,F1:F4) = 31.71054889
- =FORECAST(10,C5:F5,C6:E6) = NAN.
Related Videos
See Also
References
 is the data point .
is the data point . is the dependent array of data.
is the dependent array of data.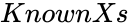 is the independent array of data.
is the independent array of data.
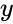 values from
values from 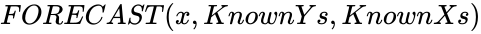 ,
, 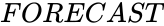 is
is 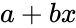
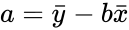 and
and 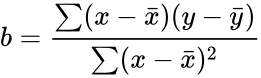 .
.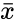 and
and 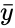 are the sample means of
are the sample means of