Difference between revisions of "Manuals/calci/PEARSON"
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''PEARSON ( | + | <div style="font-size:30px">'''PEARSON (Array1,Array2)'''</div><br/> |
| − | *<math> | + | *<math>Array1</math> is the array of independent values |
| − | *<math> | + | *<math>Array2</math> is the array of dependent values. |
| + | **PEARSON(),returns the Pearson product moment correlation coefficient. | ||
==Description== | ==Description== | ||
| − | *This function gives the Pearson | + | *This function gives the Pearson Product-Moment Correlation Coefficient. |
*It is denoted by PPMC, which shows the linear relationship between two variables. | *It is denoted by PPMC, which shows the linear relationship between two variables. | ||
*It is a measure of the strength of a linear association between two variables . | *It is a measure of the strength of a linear association between two variables . | ||
*The two variables <math> X </math> and <math> Y </math>, giving a value between +1 and −1 inclusive. | *The two variables <math> X </math> and <math> Y </math>, giving a value between +1 and −1 inclusive. | ||
| − | *Here +1 indicates the perfect positive correlation, 0 indicates no correlation | + | *Here |
| − | *The formula for PPMC,<math> r </math> is defined by: | + | +1 indicates the perfect positive correlation, |
| + | 0 indicates no correlation | ||
| + | -1 indicates the perfect negative correlation. | ||
| + | *The formula for PPMC, <math> r </math> is defined by: | ||
<math> r= \frac{ \Sigma(x-\bar{x})(y-\bar{y})}{\sqrt {\Sigma(x-\bar{x})^2(y-\bar{y})^2}}</math> | <math> r= \frac{ \Sigma(x-\bar{x})(y-\bar{y})}{\sqrt {\Sigma(x-\bar{x})^2(y-\bar{y})^2}}</math> | ||
where <math> \bar{x}</math> and <math>\bar{y} </math> are Average of the two Samples <math>x </math> and <math>y </math>. | where <math> \bar{x}</math> and <math>\bar{y} </math> are Average of the two Samples <math>x </math> and <math>y </math>. | ||
| − | *In <math>PEARSON( | + | *In <math>PEARSON(Array1,Array2)</math>, the value of <math>Array1</math> and <math>Array2</math> must be either numbers or names, array,constants or references that contain numbers. |
| − | *Suppose the array contains text,logicl values or empty cells, like that values are not considered. | + | *Suppose the array contains text, logicl values or empty cells, like that values are not considered. |
| − | *This function will return the result as error when the number of values are different for <math> | + | *This function will return the result as error when the number of values are different for <math> Array1 </math> and <math> Array2 </math>. |
==Examples== | ==Examples== | ||
| Line 44: | Line 48: | ||
|} | |} | ||
| − | =PEARSON(A1:D1,A2:D2) = | + | =PEARSON(A1:D1,A2:D2) = 0.034204238054579846 |
3. | 3. | ||
| Line 60: | Line 64: | ||
=PEARSON(A1:C1,A2:B2) = NAN | =PEARSON(A1:C1,A2:B2) = NAN | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|JO-Gc5bEG70|280|center|PEARSON}} | ||
==See Also== | ==See Also== | ||
| Line 67: | Line 75: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient Pearson] | [http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient Pearson] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:01, 8 August 2018
PEARSON (Array1,Array2)
- is the array of independent values
- is the array of dependent values.
- PEARSON(),returns the Pearson product moment correlation coefficient.
Description
- This function gives the Pearson Product-Moment Correlation Coefficient.
- It is denoted by PPMC, which shows the linear relationship between two variables.
- It is a measure of the strength of a linear association between two variables .
- The two variables and , giving a value between +1 and −1 inclusive.
- Here
+1 indicates the perfect positive correlation, 0 indicates no correlation -1 indicates the perfect negative correlation.
- The formula for PPMC, is defined by:
where and are Average of the two Samples and .
- In , the value of and must be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text, logicl values or empty cells, like that values are not considered.
- This function will return the result as error when the number of values are different for and .
Examples
| A | B | C | |
|---|---|---|---|
| 1 | 5 | 9 | 10 |
| 2 | 8 | 12 | 15 |
=PEARSON(A1:C1,A2:C2) = 0.968619605
2.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 17 | 0 | 19 | 25 |
| 2 | 10 | 11 | 7 | 13 |
=PEARSON(A1:D1,A2:D2) = 0.034204238054579846
3.
| A | B | C | |
|---|---|---|---|
| 1 | 1 | 2 | 3 |
| 2 | 4 | 5 |
=PEARSON(A1:C1,A2:B2) = NAN
Related Videos
See Also
References
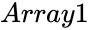 is the array of independent values
is the array of independent values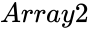 is the array of dependent values.
is the array of dependent values.