Difference between revisions of "Manuals/calci/STDEVA"
Jump to navigation
Jump to search
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''STDEVA( | + | <div style="font-size:30px">'''STDEVA()'''</div><br/> |
| − | * | + | *Parameters are set of numbers. |
| − | + | **STDEVA(), estimates standard deviation based on a sample, including numbers, text, and logical values. | |
==Description== | ==Description== | ||
| − | *This function gives the | + | *This function gives the Standard Deviation based on a given sample including the logical value and text. |
| − | *Standard | + | *Standard Deviation is a quantity expressing by how much the members of a group differ from the mean value for the group. |
*It is the used as a measure of the dispersion or variation in a distribution. | *It is the used as a measure of the dispersion or variation in a distribution. | ||
*It is calculated as the square root of variance. | *It is calculated as the square root of variance. | ||
| − | *In <math>STDEVA( | + | *In <math>STDEVA()</math>, Parameters are set of numbers to find the standard deviation. |
| − | *Here | + | *Here First parameter is required. From the second parameter are optional. |
*Instead of numbers we can use the single array or a reference of a array. | *Instead of numbers we can use the single array or a reference of a array. | ||
| − | *<math> STDEVA </math> is defined by the formula:<math>S.D= \sqrt \frac {\sum(x-\bar{x})^2}{(n-1)} </math> where <math> \bar{x} </math> is the sample mean of x and n is the total numbers in the given data. | + | *<math> STDEVA </math> is defined by the formula: |
| − | *It is calculated using | + | <math>S.D= \sqrt \frac {\sum(x-\bar{x})^2}{(n-1)} </math> |
| − | *This function | + | where <math> \bar{x} </math> is the sample mean of x and n is the total numbers in the given data. |
| − | *Suppose it | + | *It is calculated using "n-1" method. |
| + | *This function consider our given data as the sample population. | ||
| + | *Suppose it consider the data as the entire population, we can use the [[Manuals/calci/STDEVPA | STDEVPA ]] function. | ||
*The arguments can be be either numbers or names, array,constants or references that contain numbers. | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | ||
| − | *Also we can give the text representations of numbers or logical values , like TRUE or FALSE, in a | + | *Also we can give the text representations of numbers or logical values , like TRUE or FALSE, in a reference. |
| − | *Suppose the arguments containing TRUE which is | + | *Suppose the arguments containing TRUE which is evaluate as 1, and the arguments containing FALSE which is evaluate as 0. |
*Suppose the array contains the empty cells and text values like that values are not considered. | *Suppose the array contains the empty cells and text values like that values are not considered. | ||
| − | *Suppose the function don't want to consider the logical values and text representations of numbers in a reference , we can use the STDEV function. | + | *Suppose the function don't want to consider the logical values and text representations of numbers in a reference, we can use the [[Manuals/calci/STDEV | STDEV ]] function. |
*This function will return the result as error when | *This function will return the result as error when | ||
| − | 1. Any one of the argument is | + | 1. Any one of the argument is non-numeric. |
2. The arguments containing the error values or text that cannot be translated in to numbers. | 2. The arguments containing the error values or text that cannot be translated in to numbers. | ||
| − | |||
==Examples== | ==Examples== | ||
| Line 38: | Line 39: | ||
|} | |} | ||
| − | #STDEVA(A2:E2)=39.8660256358 | + | #=STDEVA(A2:E2) = 39.8660256358 |
| − | #STDEVA(A1:G1)=267.0566196431 | + | #=STDEVA(A1:G1) = 267.0566196431 |
| − | #STDEVA(4,8,TRUE) = 3.51188458428 | + | #=STDEVA(4,8,TRUE) = 3.51188458428 |
| − | #STDEVA(12,18,27,32,false)= | + | #=STDEVA(12,18,27,32,false) = 12.617448236470002 |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Related Videos== | |
| − | |||
| − | |||
| − | + | {{#ev:youtube|wJGgZJNYaPA|280|center|STANDARD DEVIATION}} | |
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/DSTDEV | DSTDEV]] | |
| − | + | *[[Manuals/calci/DSTDEVP | DSTDEVP ]] | |
| + | *[[Manuals/calci/STDEVP | STDEVP ]] | ||
| + | *[[Manuals/calci/STDEV | STDEV ]] | ||
| − | + | ==References== | |
| − | * | + | *[http://en.wikipedia.org/wiki/Standard_deviation Standard Deviation] |
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
Latest revision as of 16:18, 8 August 2018
STDEVA()
- Parameters are set of numbers.
- STDEVA(), estimates standard deviation based on a sample, including numbers, text, and logical values.
Description
- This function gives the Standard Deviation based on a given sample including the logical value and text.
- Standard Deviation is a quantity expressing by how much the members of a group differ from the mean value for the group.
- It is the used as a measure of the dispersion or variation in a distribution.
- It is calculated as the square root of variance.
- In , Parameters are set of numbers to find the standard deviation.
- Here First parameter is required. From the second parameter are optional.
- Instead of numbers we can use the single array or a reference of a array.
- is defined by the formula:
where is the sample mean of x and n is the total numbers in the given data.
- It is calculated using "n-1" method.
- This function consider our given data as the sample population.
- Suppose it consider the data as the entire population, we can use the STDEVPA function.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Also we can give the text representations of numbers or logical values , like TRUE or FALSE, in a reference.
- Suppose the arguments containing TRUE which is evaluate as 1, and the arguments containing FALSE which is evaluate as 0.
- Suppose the array contains the empty cells and text values like that values are not considered.
- Suppose the function don't want to consider the logical values and text representations of numbers in a reference, we can use the STDEV function.
- This function will return the result as error when
1. Any one of the argument is non-numeric. 2. The arguments containing the error values or text that cannot be translated in to numbers.
Examples
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | 208 | 428 | 511 | 634 | 116 | 589 | 907 |
| 2 | 18 | 25 | 76 | 91 | 107 |
- =STDEVA(A2:E2) = 39.8660256358
- =STDEVA(A1:G1) = 267.0566196431
- =STDEVA(4,8,TRUE) = 3.51188458428
- =STDEVA(12,18,27,32,false) = 12.617448236470002
Related Videos
See Also
References
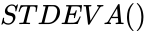 , Parameters are set of numbers to find the standard deviation.
, Parameters are set of numbers to find the standard deviation. is defined by the formula:
is defined by the formula: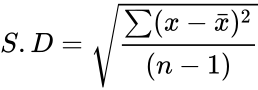 where
where 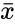 is the sample mean of x and n is the total numbers in the given data.
is the sample mean of x and n is the total numbers in the given data.