Difference between revisions of "Manuals/calci/LUCAS"
Jump to navigation
Jump to search
| (17 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''LUCAS( | + | <div style="font-size:30px">'''LUCAS (NumberUpto)'''</div><br/> |
| − | *<math> | + | *<math>NumberUpto</math> is the number indicating the position. |
| − | + | **LUCAS(),returns the sum of its two immediate previous terms. | |
==Description== | ==Description== | ||
*This function gives the Lucas series of the numbers. | *This function gives the Lucas series of the numbers. | ||
| − | *Lucas numbers are similar to the Fibonacci | + | *Lucas numbers are similar to the Fibonacci numbers. |
*It is generated by added the last two numbers in the series. | *It is generated by added the last two numbers in the series. | ||
| − | *In <math>LUCAS( | + | *In <math>LUCAS(NumberUpto)</math>, <math>NumberUpto</math> is the numbers position, which is used to displaying the numbers in the given range. |
| − | *The difference between Lucas and Fibonacci numbers are with the first two terms | + | *The difference between Lucas and Fibonacci numbers are with the first two terms <math>L_0=2</math> and <math>L_1=1 </math>, but <math>F_0=0</math> and <math>F_1=1</math>. |
| − | *The Lucas numbers are defined by: <math> | + | *The Lucas numbers are defined by: |
| − | + | <math>L_n=\begin{Bmatrix} 2 & if & n=0 \\ | |
| − | + | 1 &if & n=1 \\ | |
| − | + | L_{n-1}+L_{n-2} &if & n>1 | |
| + | \end{Bmatrix}</math> | ||
| + | *The sequence of Lucas numbers is 2,1,3,4,7,11,18,29.... | ||
| + | *The relation between Lucas and Fibonacci numbers are: | ||
| + | <math> L_n=F_n+2F_{n-1} </math> | ||
| + | and : | ||
| + | <math> F_n=\frac{L_{n-1}+L_{n+1}}{5}</math> | ||
| + | where <math>L</math> is the Lucas series with <math> L_n</math> is the <math>n^{th}</math> Lucas number and <math> F_n </math> is the <math>n^{th}</math> Fibonacci number. | ||
| + | This function will, give the result as error when <math>NumberUpto</math> is non-numeric or NumberUpto < 0 | ||
| + | |||
| + | ==Examples== | ||
| + | #=LUCAS(5) = 2 1 3 4 7 11 | ||
| + | #=LUCAS(0) = 2 | ||
| + | #=LUCAS(1) = 2 1 | ||
| + | #=LUCAS(3) = 2 1 3 4 | ||
| + | #=LUCAS(-1) = Null | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|14-NdQwKz9w|280|center|LUCAS}} | ||
| − | * | + | ==See Also== |
| − | * | + | *[[Manuals/calci/FIBONNACI| FIBONNACI]] |
| − | + | *[[Manuals/calci/PASCAL| PASCAL]] | |
| − | + | *[[Manuals/calci/FOURIERANALYSIS| FOURIERANALYSIS]] | |
| + | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Lucas_number LUCAS] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| − | + | *[[ Z3 | Z3 home ]] | |
Latest revision as of 16:26, 25 June 2018
LUCAS (NumberUpto)
- is the number indicating the position.
- LUCAS(),returns the sum of its two immediate previous terms.
Description
- This function gives the Lucas series of the numbers.
- Lucas numbers are similar to the Fibonacci numbers.
- It is generated by added the last two numbers in the series.
- In , is the numbers position, which is used to displaying the numbers in the given range.
- The difference between Lucas and Fibonacci numbers are with the first two terms and , but and .
- The Lucas numbers are defined by:
- The sequence of Lucas numbers is 2,1,3,4,7,11,18,29....
- The relation between Lucas and Fibonacci numbers are:
and : where is the Lucas series with is the Lucas number and is the Fibonacci number.
This function will, give the result as error when is non-numeric or NumberUpto < 0
Examples
- =LUCAS(5) = 2 1 3 4 7 11
- =LUCAS(0) = 2
- =LUCAS(1) = 2 1
- =LUCAS(3) = 2 1 3 4
- =LUCAS(-1) = Null
Related Videos
See Also
References
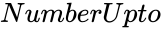 is the number indicating the position.
is the number indicating the position.
 ,
, 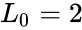 and
and 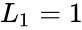 , but
, but 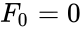 and
and 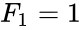 .
.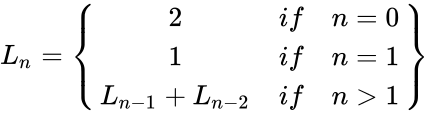
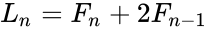 and :
and :
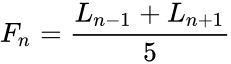 where
where 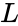 is the Lucas series with
is the Lucas series with 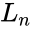 is the
is the 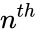 Lucas number and
Lucas number and 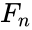 is the
is the