Difference between revisions of "Manuals/calci/BINOMIAL"
Jump to navigation
Jump to search
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''BINOMIAL( | + | <div style="font-size:30px">'''BINOMIAL(N,K)'''</div><br/> |
| − | *<math> | + | *<math>N</math> is the number of items. |
| − | *<math> | + | *<math>K </math> is the number of selection. |
| Line 25: | Line 25: | ||
*Most compact formula for the coefficient of the binomial value is Factorial formula. | *Most compact formula for the coefficient of the binomial value is Factorial formula. | ||
*Factorial formula is symmetric of the combination formula. | *Factorial formula is symmetric of the combination formula. | ||
| + | |||
| + | ==ZOS== | ||
| + | |||
| + | *The syntax is to calculate BINOMIAL in ZOS is <math>BINOMIAL (N,K)</math>. | ||
| + | **<math>N</math> is the number of items. | ||
| + | **<math>K</math> is the number of selection. | ||
| + | *For e.g., BINOMIAL(20..25,4) | ||
| + | *BINOMIAL(10..14,7..8) | ||
==Examples== | ==Examples== | ||
| Line 44: | Line 52: | ||
*[http://en.wikipedia.org/wiki/Binomial_distribution Binomial Distribution] | *[http://en.wikipedia.org/wiki/Binomial_distribution Binomial Distribution] | ||
*[http://en.wikipedia.org/wiki/Binomial_coefficient Binomial Coefficient] | *[http://en.wikipedia.org/wiki/Binomial_coefficient Binomial Coefficient] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:11, 5 June 2018
BINOMIAL(N,K)
- is the number of items.
- is the number of selection.
Description
- This function gives the coefficent of the binomial distribution.
- Binomial coefficient is the set of positive integer which equals the number of combinations of k items that can be selected from a set of n items.
- The coefficients satisfy the Pascals recurrence.
- The binomial coefficents are denoted by and it is read by n choose k.
- It is the coefficient of the term in the polynomial expansion of the binomial thorem .
- The coefficient is occur in the formula of binomial thorem:
where .
- To find the coefficient of the binomial ,we can use several methods.
1. Recursive formula 2. Multiplicative formula 3. Factorial formula.
- 1.Recursive Formula:
for and .
- 2. Multiplicative formula:
- 3.Factorial formula:
where ,and which is zero when .
- Also for the initial values for .
- Most compact formula for the coefficient of the binomial value is Factorial formula.
- Factorial formula is symmetric of the combination formula.
ZOS
- The syntax is to calculate BINOMIAL in ZOS is .
- is the number of items.
- is the number of selection.
- For e.g., BINOMIAL(20..25,4)
- BINOMIAL(10..14,7..8)
Examples
- =BINOMIAL(10,3)= 120
- =BINOMIAL(20,7)= 77520
- =BINOMIAL(15,0)= 1
- =BINOMIAL(12,12)=1
- =BINOMIAL(1,-1) = 0
Related Videos
See Also
References
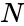 is the number of items.
is the number of items. is the number of selection.
is the number of selection.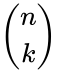 and it is read by n choose k.
and it is read by n choose k.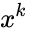 term in the polynomial expansion of the binomial thorem
term in the polynomial expansion of the binomial thorem 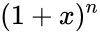 .
.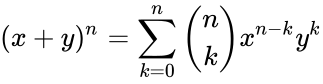 where
where  .
.
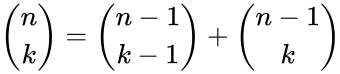 for
for  and
and  .
.
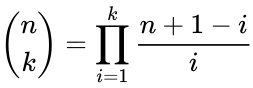
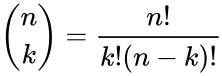 where
where  .
.
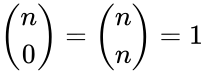 for
for 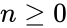 .
.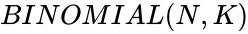 .
.