Difference between revisions of "Manuals/calci/ARROWHEAD"
Jump to navigation
Jump to search
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''MATRIX(" | + | <div style="font-size:30px">'''MATRIX("ARROWHEAD",order)'''</div><br/> |
*<math>order</math> is the order of the arrowhead matrix. | *<math>order</math> is the order of the arrowhead matrix. | ||
| Line 5: | Line 5: | ||
*This function returns the matrix with the type arrowhead. | *This function returns the matrix with the type arrowhead. | ||
*In mathematical, a square matrix containing zeros in all entries except for the first row first column and main diagonal. | *In mathematical, a square matrix containing zeros in all entries except for the first row first column and main diagonal. | ||
| − | *i.e., The matrix of the form | + | *i.e., The matrix of the form |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
A= <math>\begin{bmatrix} | A= <math>\begin{bmatrix} | ||
* & * & *& * & * \\ | * & * & *& * & * \\ | ||
* & * & 0 & 0 & 0 \\ | * & * & 0 & 0 & 0 \\ | ||
| − | * & 0 & * & 0 & 0 \\ | + | * & 0 & * & 0 & 0 \\ |
| + | * & 0 & 0 & * & 0 \\ | ||
| + | * & 0 & 0 & 0 & * \\ | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
| − | *So | + | *So Calci displays, the elements of the arrowhead matirx are 1 except 1st row and column and main diagonal. |
*The matrix has the form Any symmetric permutation of the arrowhead matrix, where P is a permutation matrix is a arrowhead matrix. | *The matrix has the form Any symmetric permutation of the arrowhead matrix, where P is a permutation matrix is a arrowhead matrix. | ||
| − | *i.e.,P^T A P where P is a permutation matrix is a arrowhead matrix. | + | *i.e.,<math>P^T A P</math> where P is a permutation matrix is a arrowhead matrix. |
*Real symmetric arrowhead matrices are often an essential tool for the computation of the eigenvalues | *Real symmetric arrowhead matrices are often an essential tool for the computation of the eigenvalues | ||
| + | |||
| + | ==Examples== | ||
| + | *MATRIX("arrowhead") = 1 | ||
| + | *MATRIX("arrowhead",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || 1 || 0 | ||
| + | |- | ||
| + | | 1 || 0 || 1 | ||
| + | |} | ||
| + | *MATRIX("arrowhead",5) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || 1 || 0 || 0 ||0 | ||
| + | |- | ||
| + | | 1 || 0 || 1 || 0 || 0 | ||
| + | |- | ||
| + | | 1 || 0 || 0 || 1 || 0 | ||
| + | |- | ||
| + | | 1 || 0 || 0 || 0 ||1 | ||
| + | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Arrowhead_matrix Arrowhead] | ||
Latest revision as of 00:21, 26 October 2015
MATRIX("ARROWHEAD",order)
- is the order of the arrowhead matrix.
Description
- This function returns the matrix with the type arrowhead.
- In mathematical, a square matrix containing zeros in all entries except for the first row first column and main diagonal.
- i.e., The matrix of the form
A=
- So Calci displays, the elements of the arrowhead matirx are 1 except 1st row and column and main diagonal.
- The matrix has the form Any symmetric permutation of the arrowhead matrix, where P is a permutation matrix is a arrowhead matrix.
- i.e., where P is a permutation matrix is a arrowhead matrix.
- Real symmetric arrowhead matrices are often an essential tool for the computation of the eigenvalues
Examples
- MATRIX("arrowhead") = 1
- MATRIX("arrowhead",3)
| 1 | 1 | 1 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
- MATRIX("arrowhead",5)
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
 is the order of the arrowhead matrix.
is the order of the arrowhead matrix.
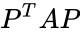 where P is a permutation matrix is a arrowhead matrix.
where P is a permutation matrix is a arrowhead matrix.