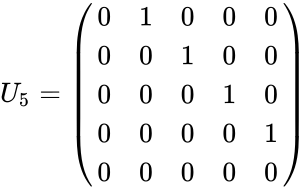Difference between revisions of "Manuals/calci/SHIFT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''SHIFT'''</div><br/>") |
|||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''SHIFT'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("SHIFT",order)'''</div><br/> |
| + | *<math>order</math> is the size of the Shift matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function returns shift matrix of order 3. | ||
| + | *A shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. | ||
| + | *A shift matrix U with ones on the superdiagonal is an upper shift matrix. | ||
| + | *The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix. | ||
| + | *Let Z is a shift matrix , then <math>ZA, Z^TA, AZ, AZ^T, ZAZ^T</math> are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively. | ||
| + | *The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix. | ||
| + | *The <math>(i,j)^{th}</math> component of U and L are: | ||
| + | <math>U_{ij} = \delta_{i+1,j}, \quad L_{ij} = \delta_{i,j+1}</math>. | ||
| + | where <math>\delta_{ij}</math> is the Kronecker delta symbol. | ||
| + | *For example, the 5×5 shift matrices are | ||
| + | <math>U_5=\begin{pmatrix} | ||
| + | 0 & 1 & 0 & 0 & 0 \\ | ||
| + | 0 & 0 & 1 & 0 & 0 \\ | ||
| + | 0 & 0 & 0 & 1 & 0 \\ | ||
| + | 0 & 0 & 0 & 0 & 1 \\ | ||
| + | 0 & 0 & 0 & 0 & 0 | ||
| + | \end{pmatrix}</math> | ||
| + | <math>L_5 = \begin{pmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 \\ | ||
| + | 1 & 0 & 0 & 0 & 0 \\ | ||
| + | 0 & 1 & 0 & 0 & 0 \\ | ||
| + | 0 & 0 & 1 & 0 & 0 \\ | ||
| + | 0 & 0 & 0 & 0 & 0 | ||
| + | \end{pmatrix}</math> | ||
| + | *All shift matrices are nilpotent; an n by n shift matrix S becomes the null matrix when raised to the power of its dimension n. | ||
| + | |||
| + | |||
| + | ==Examples== | ||
| + | *1.MATRIX("shift") = 0 | ||
| + | *2.MATRIX("shift",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 1 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 1 | ||
| + | |- | ||
| + | | 0 || 0 || 0 | ||
| + | |} | ||
| + | *3.MATRIX("shift",7) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 1 || 0 || 0 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 1 || 0 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 1 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 0 || 1 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 0 || 0 || 1 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 0 || 0 || 0 || 1 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| + | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/SIGNATURE| SIGNATURE]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/TRIANGULAR| TRIANGULAR]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Shift_matrix Shift Matrix] | ||
Latest revision as of 01:39, 26 October 2015
MATRIX("SHIFT",order)
- is the size of the Shift matrix.
Description
- This function returns shift matrix of order 3.
- A shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere.
- A shift matrix U with ones on the superdiagonal is an upper shift matrix.
- The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix.
- Let Z is a shift matrix , then are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively.
- The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix.
- The component of U and L are:
.
where is the Kronecker delta symbol.
- For example, the 5×5 shift matrices are
- All shift matrices are nilpotent; an n by n shift matrix S becomes the null matrix when raised to the power of its dimension n.
Examples
- 1.MATRIX("shift") = 0
- 2.MATRIX("shift",3)
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 0 | 0 | 0 |
- 3.MATRIX("shift",7)
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
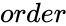 is the size of the Shift matrix.
is the size of the Shift matrix.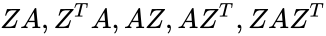 are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively.
are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively.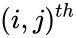 component of U and L are:
component of U and L are: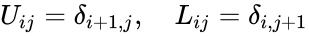 .
.
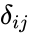 is the Kronecker delta symbol.
is the Kronecker delta symbol.