Difference between revisions of "Manuals/calci/PERMUTATION"
Jump to navigation
Jump to search
| (9 intermediate revisions by 3 users not shown) | |||
| Line 8: | Line 8: | ||
*A permutation matrix is nonsingular, and its determiant + or -. | *A permutation matrix is nonsingular, and its determiant + or -. | ||
*Also permutation matrix A having the following properties <math>AA^T=I</math>, where <math>A^T</math> is a transpose and I is the identity matrix. | *Also permutation matrix A having the following properties <math>AA^T=I</math>, where <math>A^T</math> is a transpose and I is the identity matrix. | ||
| − | *Permutation matrices are orthogonal | + | *Permutation matrices are orthogonal .Hence, their inverse is their transpose: <math>P^{-1} = P^T</math>. |
*A permutation matrix allows to exchange rows or columns of another via the matrix-matrix product. | *A permutation matrix allows to exchange rows or columns of another via the matrix-matrix product. | ||
*In calci MATRIX("permutation",4) gives the permutation matrix of order 4. | *In calci MATRIX("permutation",4) gives the permutation matrix of order 4. | ||
| + | |||
| + | ==Examples== | ||
| + | *1.MATRIX("permutation",5,200..210) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 200 || 0 | ||
| + | |- | ||
| + | | 0 || 201 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 202 || 0 || 0 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 203 || 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 || 0 || 0 || 204 | ||
| + | |} | ||
| + | *2.MATRIX("permutation",18).<math>\$</math>_(SUM) = 18 | ||
| + | *3.MATRIX("permutation",5).<math>\$$$</math>(SUM)= | ||
| + | {|class="wikitable" | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |} | ||
| + | *4.MATRIX("permutation",5).<math>\$$</math>(SUM) = | ||
| + | {|class="wikitable" | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|lOjawd_NzMA|280|center|Permutation Matrix}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/PASCAL| PASCAL]] | ||
| + | *[[Manuals/calci/HANKEL| HANKEL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Permutation_matrix Permutation Matrix] | ||
Latest revision as of 01:35, 26 October 2015
MATRIX("PERMUTATION",order)
- is the size of the Permutation matrix.
Description
- This function returns the matrix Permutation matrix of order 3.
- A permutation matrix is a square binary matrix obtained by permuting the rows of an nxn identity matrix according to some permutation of the numbers 1 to n.
- This matrix has exactly one entry 1 in each row and each column and 0's elsewhere.
- A permutation matrix is nonsingular, and its determiant + or -.
- Also permutation matrix A having the following properties , where is a transpose and I is the identity matrix.
- Permutation matrices are orthogonal .Hence, their inverse is their transpose: .
- A permutation matrix allows to exchange rows or columns of another via the matrix-matrix product.
- In calci MATRIX("permutation",4) gives the permutation matrix of order 4.
Examples
- 1.MATRIX("permutation",5,200..210)
| 0 | 0 | 0 | 200 | 0 |
| 0 | 201 | 0 | 0 | 0 |
| 202 | 0 | 0 | 0 | 0 |
| 0 | 0 | 203 | 0 | 0 |
| 0 | 0 | 0 | 0 | 204 |
- 2.MATRIX("permutation",18)._(SUM) = 18
- 3.MATRIX("permutation",5).(SUM)=
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
- 4.MATRIX("permutation",5).(SUM) =
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
 is the size of the Permutation matrix.
is the size of the Permutation matrix.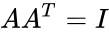 , where
, where 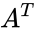 is a transpose and I is the identity matrix.
is a transpose and I is the identity matrix.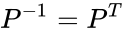 .
. _(SUM) = 18
_(SUM) = 18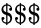 (SUM)=
(SUM)=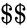 (SUM) =
(SUM) =