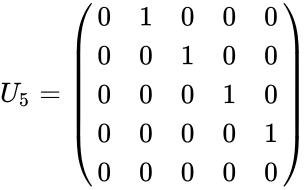Difference between revisions of "Manuals/calci/SHIFT"
Jump to navigation
Jump to search
| (One intermediate revision by the same user not shown) | |||
| Line 31: | Line 31: | ||
==Examples== | ==Examples== | ||
| − | *1.MATRIX("shift") | + | *1.MATRIX("shift") = 0 |
| + | *2.MATRIX("shift",3) | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 40: | Line 41: | ||
| 0 || 0 || 0 | | 0 || 0 || 0 | ||
|} | |} | ||
| − | * | + | *3.MATRIX("shift",7) |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 64: | Line 65: | ||
==References== | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Shift_matrix Shift Matrix] | ||
Latest revision as of 01:39, 26 October 2015
MATRIX("SHIFT",order)
- is the size of the Shift matrix.
Description
- This function returns shift matrix of order 3.
- A shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere.
- A shift matrix U with ones on the superdiagonal is an upper shift matrix.
- The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix.
- Let Z is a shift matrix , then are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively.
- The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix.
- The component of U and L are:
.
where is the Kronecker delta symbol.
- For example, the 5×5 shift matrices are
- All shift matrices are nilpotent; an n by n shift matrix S becomes the null matrix when raised to the power of its dimension n.
Examples
- 1.MATRIX("shift") = 0
- 2.MATRIX("shift",3)
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 0 | 0 | 0 |
- 3.MATRIX("shift",7)
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
 is the size of the Shift matrix.
is the size of the Shift matrix.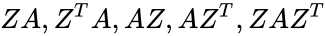 are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively.
are equal to the matrix A shifted one position down, up left, right, and down along the main diagonal respectively. component of U and L are:
component of U and L are: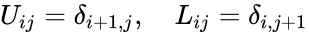 .
.
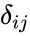 is the Kronecker delta symbol.
is the Kronecker delta symbol.