Difference between revisions of "Manuals/calci/DET"
Jump to navigation
Jump to search
| (One intermediate revision by the same user not shown) | |||
| Line 47: | Line 47: | ||
#=DET([[1,0,2,1],[4,0,2,-1],[1,4,5,2],[3,1,2,0]]) = 17 | #=DET([[1,0,2,1],[4,0,2,-1],[1,4,5,2],[3,1,2,0]]) = 17 | ||
#=DET([1,2,3],[5,2,8]) = NAN | #=DET([1,2,3],[5,2,8]) = NAN | ||
| + | |||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=H9BWRYJNIv4|280|center|Determinants}} | ||
| Line 54: | Line 59: | ||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/Determinant Determinant ] | + | *[http://en.wikipedia.org/wiki/Determinant Determinant ] |
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 04:43, 26 May 2020
DET(array)
- is the set of numbers.
Description
- This function gives the determinant value of a matrix.
- To calculate the determinant of a matrix, we can choose only square matrix.i.e. Number of rows and number of columns should be equal.
- Determinant of the identity matrix is always 1.
- Determinant of the matrix is denoted by or .
- Let be 2x2 matrix with the elements
- Then , where all are real numbers.
- Let be the 3x3 matrix with the elements
Then :
- Let be a square matrix of order . Write ,
- Where is the entry on the row and column and to & to .
- For any and , set (called the co-factors), then the general formula for determinant of the matrix is,
, for any fixed . Also, for any fixed .
- This function will give the result as error when
1. Any one of the element in array is empty or contain non-numeric 2. Number of rows is not equal to number of columns
Examples
- =DET([[6,4,8],[3,6,1],[2,4,5]]) = 104
- =DET([[-5,10],[6,-8]]) = -20
- =DET([[1,0,2,1],[4,0,2,-1],[1,4,5,2],[3,1,2,0]]) = 17
- =DET([1,2,3],[5,2,8]) = NAN
Related Videos
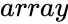 is the set of numbers.
is the set of numbers. is denoted by
is denoted by 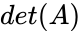 or
or 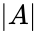 .
.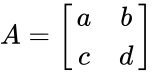
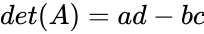 , where
, where  all are real numbers.
all are real numbers.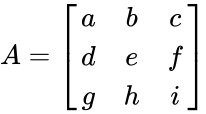 Then
Then 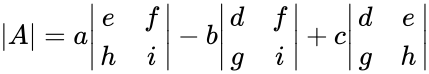 :
:
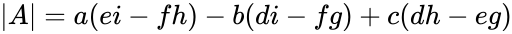
 . Write
. Write 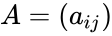 ,
,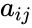 is the entry on the
is the entry on the 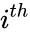 row and
row and 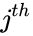 column and
column and 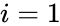 to
to 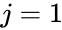 to
to  and
and 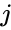 , set
, set 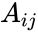 (called the co-factors), then the general formula for determinant of the matrix
(called the co-factors), then the general formula for determinant of the matrix 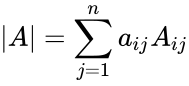 , for any fixed
, for any fixed 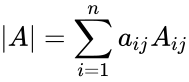 , for any fixed
, for any fixed