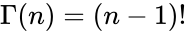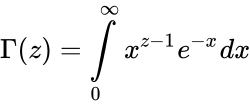Difference between revisions of "Manuals/calci/GAMMAFUNCTION"
Jump to navigation
Jump to search
(Created page with "==gamma==") |
|||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:30px">'''GAMMAFUNCTION (z)'''</div><br/> |
| + | *<math>z</math> is any positive real number. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the value of the Gamma function. | ||
| + | *The Gamma function is defined to be an extension of the factorial to complex and real number arguments. | ||
| + | *That is, if n is a positive integer: | ||
| + | <math>\Gamma (n)=(n-1)!</math> | ||
| + | *Gamma function is defined for all complex numbers except the non-positive integers. | ||
| + | *For complex numbers with a positive real part, it is defined via a convergent improper integral: | ||
| + | <math>\Gamma (z) = \int\limits_{0}^{\infty} x^{z-1} e^{-x} dx </math> | ||
| + | *This function will return the result as NaN when the given number as negative or Non numeric. | ||
| + | |||
| + | |||
| + | ==Examples== | ||
| + | #GAMMAFUNCTION(2) = 1.0000026676984093 | ||
| + | #GAMMAFUNCTION(45.3) = 8.308990531109891e+54 | ||
| + | #GAMMAFUNCTION(-3) = #N/A (#NUM!) | ||
| + | |||
| + | ==Related Videos== | ||
| + | {{#ev:youtube|v=XZIVrkkYBRI|280|center|Gamma Function}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/GAMMADIST | GAMMADIST]] | ||
| + | *[[Manuals/calci/SUM | SUM ]] | ||
| + | |||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Gamma_function Gamma Function] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 03:55, 12 August 2020
GAMMAFUNCTION (z)
- is any positive real number.
Description
- This function gives the value of the Gamma function.
- The Gamma function is defined to be an extension of the factorial to complex and real number arguments.
- That is, if n is a positive integer:
- Gamma function is defined for all complex numbers except the non-positive integers.
- For complex numbers with a positive real part, it is defined via a convergent improper integral:
- This function will return the result as NaN when the given number as negative or Non numeric.
Examples
- GAMMAFUNCTION(2) = 1.0000026676984093
- GAMMAFUNCTION(45.3) = 8.308990531109891e+54
- GAMMAFUNCTION(-3) = #N/A (#NUM!)
Related Videos
See Also
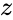 is any positive real number.
is any positive real number.