Difference between revisions of "Manuals/calci/PERMUTATIONS"
Jump to navigation
Jump to search
| (9 intermediate revisions by 2 users not shown) | |||
| Line 9: | Line 9: | ||
*Maxcount is the maximum number of counts to find the Permutation. | *Maxcount is the maximum number of counts to find the Permutation. | ||
*A formula for the number of possible permutations of k objects from a set of n. <math>n_pK or P(n,k)=\frac{n!}{(n-k)!} </math> | *A formula for the number of possible permutations of k objects from a set of n. <math>n_pK or P(n,k)=\frac{n!}{(n-k)!} </math> | ||
| + | |||
| + | ==Examples== | ||
| + | 1. PERMUTATIONS([3,4,5,6],3) | ||
| + | 3 4 5 | ||
| + | 3 4 6 | ||
| + | 3 5 4 | ||
| + | 3 5 6 | ||
| + | 3 6 4 | ||
| + | 3 6 5 | ||
| + | 4 3 5 | ||
| + | 4 3 6 | ||
| + | 4 5 3 | ||
| + | 4 5 6 | ||
| + | 4 6 3 | ||
| + | 4 6 5 | ||
| + | 5 3 4 | ||
| + | 5 3 6 | ||
| + | 5 4 3 | ||
| + | 5 4 6 | ||
| + | 5 6 3 | ||
| + | 5 6 4 | ||
| + | 6 3 4 | ||
| + | 6 3 5 | ||
| + | 6 4 3 | ||
| + | 6 4 5 | ||
| + | 6 5 3 | ||
| + | 6 5 4 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=DROZVHObeko|280|center|Permutations}} | ||
| + | |||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/PERMUT | PERMUT]] | ||
| + | *[[Manuals/calci/COMBIN | COMBIN ]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Permutation Permutation] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 23:59, 15 April 2020
PERMUTATIONS (List,Of,MaxCount,IsAsString)
- are set of real numbers.
- maximum number of counts.
Description
- This function returns the Permutation list of the given number.
- A permutation, also called an "arrangement number" or "order," is a rearrangement of the elements of an ordered in a list.
- In PERMUTATIONS(List,Of,MaxCount,IsAsString),List is the set of numbers to find the Permutation.
- Maxcount is the maximum number of counts to find the Permutation.
- A formula for the number of possible permutations of k objects from a set of n.
Examples
1. PERMUTATIONS([3,4,5,6],3)
3 4 5 3 4 6 3 5 4 3 5 6 3 6 4 3 6 5 4 3 5 4 3 6 4 5 3 4 5 6 4 6 3 4 6 5 5 3 4 5 3 6 5 4 3 5 4 6 5 6 3 5 6 4 6 3 4 6 3 5 6 4 3 6 4 5 6 5 3 6 5 4
Related Videos
See Also
References
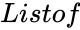 are set of real numbers.
are set of real numbers.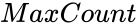 maximum number of counts.
maximum number of counts.