Difference between revisions of "Manuals/calci/KFUNCTION"
(Created page with "kfun") |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <div style="font-size:30px">'''KFUNCTION (Number)'''</div><br/> | |
| + | *<math>Number</math> is any real number. | ||
| + | |||
| + | ==Description== | ||
| + | *This function shows the value of the K function. | ||
| + | *In <math>KFUNCTION(Number)</math>,Number is any real number. | ||
| + | *K function is named as Ripley's K Function. | ||
| + | *It is defined as how the spatial clustering or dispersion of feature centroids changes when the neighborhood size changes. | ||
| + | *When using this tool, specify the number of distances to evaluate and, optionally, a starting distance and/or distance increment. | ||
| + | *The K-Function is given as : | ||
| + | <math>L(d)=\frac{\sqrt{A \sum_{i=1}^n \sum_{j=1,j\neq i}^n k(i,j)}}{\pi n(n-1)}</math> | ||
| + | Where d is the distance, n is equal to the total number of features. | ||
| + | *<math>A</math> represents the total area of the features and <math>k_{i,j}</math> is a weight. | ||
| + | *If there is no edge correction, then the weight will be equal to one when the distance between i and j is less than d, and will equate to zero otherwise. | ||
| + | |||
| + | ==Examples== | ||
| + | # KFUNCTION(5) = 27648 | ||
| + | # KFUNCTION(15) = 1.8473984485535928e+99 | ||
| + | # KFUNCTION(6.453) = 86400000 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=Uz0MtFlLD-k|280|center|Relations and Functions}} | ||
| + | |||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | *[[Manuals/calci/SUM | SUM]] | ||
| + | *[[Manuals/calci/SQRT | SQRT]] | ||
| + | |||
| + | ==References== | ||
| + | [http://resources.esri.com/help/9.3/arcgisdesktop/com/gp_toolref/spatial_statistics_tools/how_multi_distance_spatial_cluster_analysis_colon_ripley_s_k_function_spatial_statistics_works.htm K Function] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 17:16, 5 December 2018
KFUNCTION (Number)
- is any real number.
Description
- This function shows the value of the K function.
- In ,Number is any real number.
- K function is named as Ripley's K Function.
- It is defined as how the spatial clustering or dispersion of feature centroids changes when the neighborhood size changes.
- When using this tool, specify the number of distances to evaluate and, optionally, a starting distance and/or distance increment.
- The K-Function is given as :
Where d is the distance, n is equal to the total number of features.
- represents the total area of the features and is a weight.
- If there is no edge correction, then the weight will be equal to one when the distance between i and j is less than d, and will equate to zero otherwise.
Examples
- KFUNCTION(5) = 27648
- KFUNCTION(15) = 1.8473984485535928e+99
- KFUNCTION(6.453) = 86400000
Related Videos
See Also
References
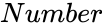 is any real number.
is any real number.