Difference between revisions of "Manuals/calci/CROSSPRODUCT"
Jump to navigation
Jump to search
| (7 intermediate revisions by 2 users not shown) | |||
| Line 7: | Line 7: | ||
*The cross product is defined in three dimensional space and it is denoted by axb. | *The cross product is defined in three dimensional space and it is denoted by axb. | ||
*In CROSSPRODUCT (a,b), a and b are any two positive real numbers. | *In CROSSPRODUCT (a,b), a and b are any two positive real numbers. | ||
| − | *We can calculate the Cross Product this way:<math> | + | *We can calculate the Cross Product this way: |
| + | *<math>a X b</math> = <math>\mid a\mid</math>.<math> \mid b\mid</math><math> sin(\theta) n</math> | ||
*<math>\mid a\mid</math> is the magnitude (length) of vector a | *<math>\mid a\mid</math> is the magnitude (length) of vector a | ||
*<math>\mid b</math> is the magnitude (length) of vector b | *<math>\mid b</math> is the magnitude (length) of vector b | ||
*<math>\theta</math> is the angle between a and b | *<math>\theta</math> is the angle between a and b | ||
| − | *n is the unit vector at right angles to both a and b | + | *<math>n</math> is the unit vector at right angles to both a and b. |
| + | |||
| + | ==Examples== | ||
| + | #CROSSPRODUCT([2,7,8],[3,9,5]) =-37 14 -3 | ||
| + | #CROSSPRODUCT([3,8,-2],[10,6,-5]) = -28 -5 -62 | ||
| + | #CROSSPRODUCT([5.2,9.1,-4],[4,6,8]) = 96.8 -57.6 -5.199999999999996 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=pWbOisq1MJU|280|center|Cross Product}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/DOTPRODUCT | DOTPRODUCT]] | ||
| + | *[[Manuals/calci/CARTESIANPRODUCT | CARTESIANPRODUCT ]] | ||
| + | |||
| + | ==References== | ||
| + | [https://www.mathsisfun.com/algebra/vectors-cross-product.html Cross Product] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:20, 11 December 2018
CROSSPRODUCT (a,b)
- and are any real numbers.
Description
- This function shows the Cross product of two numbers.
- Cross product is also called Vector product.
- The cross product is defined in three dimensional space and it is denoted by axb.
- In CROSSPRODUCT (a,b), a and b are any two positive real numbers.
- We can calculate the Cross Product this way:
- = .
- is the magnitude (length) of vector a
- is the magnitude (length) of vector b
- is the angle between a and b
- is the unit vector at right angles to both a and b.
Examples
- CROSSPRODUCT([2,7,8],[3,9,5]) =-37 14 -3
- CROSSPRODUCT([3,8,-2],[10,6,-5]) = -28 -5 -62
- CROSSPRODUCT([5.2,9.1,-4],[4,6,8]) = 96.8 -57.6 -5.199999999999996
Related Videos
See Also
References
 and
and  are any real numbers.
are any real numbers.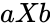 =
= 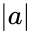 .
.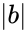
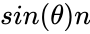
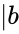 is the magnitude (length) of vector b
is the magnitude (length) of vector b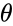 is the angle between a and b
is the angle between a and b is the unit vector at right angles to both a and b.
is the unit vector at right angles to both a and b.