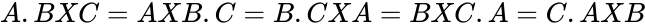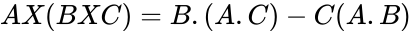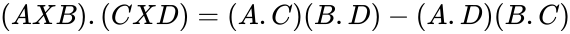Difference between revisions of "Manuals/calci/DYADIC"
Jump to navigation
Jump to search
| (6 intermediate revisions by 2 users not shown) | |||
| Line 20: | Line 20: | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
*The direct product is non-commutative <math>(AB \neq BA)</math>. | *The direct product is non-commutative <math>(AB \neq BA)</math>. | ||
| − | *A few vector product identities are of interest | + | *A few vector product identities are of interest: |
| + | #<math>A.BXC = AXB.C=B.CXA=BXC.A=C.AXB</math> | ||
| + | #<math>AX(BXC)= B.(A.C)- C(A.B)</math> | ||
| + | #<math>(AXB)XC = B(A.C)-A(B.C)</math> | ||
| + | #<math>(AXB).(CXD)= (A.C)(B.D)-(A.D)(B.C)</math> | ||
| + | #<math>(AXB).(CXD) = (AxB.D)C-(AxB.C)D</math> | ||
| + | |||
| + | ==Examples== | ||
| + | #DYADIC([1,2,3],[8,7,6]) = 40 | ||
| + | #VECTORDIRECTPRODUCT([14,17,20],[22,26,5]) = 850 | ||
| + | #VECTORDIRECTPRODUCT([2.7,3.9,10.2],[14.5,19,-4]) = 72.45 | ||
| + | #DYADIC([-8,-4,2],[10,-45,67]) = 234 | ||
| + | |||
| + | ==Related Videos== | ||
| + | {{#ev:youtube|v=tpL95Sd7zT0|280|center|Tensor Product}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/DOTPRODUCT | DOTPRODUCT ]] | ||
| + | *[[Manuals/calci/CROSSPRODUCT | CROSSPRODUCT ]] | ||
| + | *[[Manuals/calci/CARTESIANPRODUCT | CARTESIANPRODUCT ]] | ||
| + | |||
| + | ==References== | ||
| + | [http://www.pgccphy.net/ref/vprod.pdf Direct Product] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:41, 10 January 2019
DYADIC(a,b)
OR VECTORDIRECTPRODUCT (a,b)
- and any two set of values.
Description
- This function shows the Vector Direct product.
- The third type of vector multiplication is called the direct product, and is written AB.
- In , and are the two vectors.
- Multiplying one vector by another under the direct product gives a tensor result.
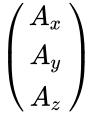
- The rectangular components of the direct product may be found by matrix multiplication: one multiplies the column vector A by the transpose of B, which gives a 3X3 matrix:
= =
- The direct product is non-commutative .
- A few vector product identities are of interest:
Examples
- DYADIC([1,2,3],[8,7,6]) = 40
- VECTORDIRECTPRODUCT([14,17,20],[22,26,5]) = 850
- VECTORDIRECTPRODUCT([2.7,3.9,10.2],[14.5,19,-4]) = 72.45
- DYADIC([-8,-4,2],[10,-45,67]) = 234
Related Videos
See Also
References
 and
and  any two set of values.
any two set of values.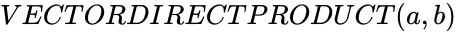 ,
, 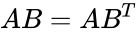 =
=
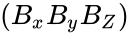 =
=
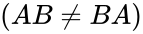 .
.