Difference between revisions of "Manuals/calci/STEYX"
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''STEYX( | + | <div style="font-size:30px">'''STEYX (KnownYs,KnownXs) '''</div><br/> |
| − | *<math> | + | *<math>KnownYs</math> is set of dependent values. |
| − | *<math> | + | *<math>KnownXs </math> is the set of independent values. |
| + | **STEYX(),returns the standard error of the predicted y-value for each x in the regression. | ||
==Description== | ==Description== | ||
*This function gives the standard error of the regression, which also is known as the standard error of the estimate. | *This function gives the standard error of the regression, which also is known as the standard error of the estimate. | ||
| − | *It is calculates the standard error for the straight line of best fit through a supplied set of <math> | + | *It is calculates the standard error for the straight line of best fit through a supplied set of <math> KnownXs</math> and <math> KnownYs</math> values. |
| − | *The standard error for this line provides a measure of the error in the prediction of <math> | + | *The standard error for this line provides a measure of the error in the prediction of <math> KnownYs </math> for an individual <math> KnownXs </math>. |
*The equation for the standard error of the predicted <math> y </math> is: | *The equation for the standard error of the predicted <math> y </math> is: | ||
<math>\sqrt{\frac{1}{(n-2)}\left [ \sum(y-\bar{y})^2-\frac{[\sum(x-\bar{x})(y-\bar{y})]^2}{\sum(x-\bar{x})^2} \right ]}</math> | <math>\sqrt{\frac{1}{(n-2)}\left [ \sum(y-\bar{y})^2-\frac{[\sum(x-\bar{x})(y-\bar{y})]^2}{\sum(x-\bar{x})^2} \right ]}</math> | ||
where <math>\bar{x}</math> and <math>\bar{y}</math> are the sample mean <math> x </math> and <math> y </math>. | where <math>\bar{x}</math> and <math>\bar{y}</math> are the sample mean <math> x </math> and <math> y </math>. | ||
| − | *In <math> STEYX( | + | *In <math>STEYX (KnownYs,KnownXs)</math>, <math>KnownYs </math> is the array of the numeric dependent values and <math> KnownXs </math> is the array of the independent values. |
*The arguments can be be either numbers or names, array,constants or references that contain numbers. | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | ||
*Suppose the array contains text,logical values or empty cells, like that values are not considered. | *Suppose the array contains text,logical values or empty cells, like that values are not considered. | ||
*This function will return the result as error when | *This function will return the result as error when | ||
1. Any one of the argument is non-numeric. | 1. Any one of the argument is non-numeric. | ||
| − | 2. | + | 2. KnownYs and KnownXs are empty or that have less than three data points. |
| − | 3. | + | 3. KnownYs and KnownXs have a different number of data points. |
==Examples== | ==Examples== | ||
Latest revision as of 13:58, 18 June 2018
STEYX (KnownYs,KnownXs)
- is set of dependent values.
- is the set of independent values.
- STEYX(),returns the standard error of the predicted y-value for each x in the regression.
Description
- This function gives the standard error of the regression, which also is known as the standard error of the estimate.
- It is calculates the standard error for the straight line of best fit through a supplied set of and values.
- The standard error for this line provides a measure of the error in the prediction of for an individual .
- The equation for the standard error of the predicted is:
where and are the sample mean and .
- In , is the array of the numeric dependent values and is the array of the independent values.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logical values or empty cells, like that values are not considered.
- This function will return the result as error when
1. Any one of the argument is non-numeric. 2. KnownYs and KnownXs are empty or that have less than three data points. 3. KnownYs and KnownXs have a different number of data points.
Examples
1.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 6 | 8 | 10 | 13 | 15 | 5 |
| 2 | 1 | 4 | 8 | 11 | 20 | 3 |
=STEYX(A1:F1,A2:F2) = 1.4525201161135368
2.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 2 | 9 | 1 | 8 | 17 |
| 2 | 10 | 4 | 11 | 2 | 6 |
=STEYX(A1:E1,A2:E2)) = 5.944184833375669
3.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 4 | 5 | 8 |
| 2 | 10 | 4 | 7 | 5 |
=STEYX(A1:A5,B1:B4) = NAN
Related Videos
See Also
References
 is set of dependent values.
is set of dependent values.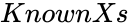 is the set of independent values.
is the set of independent values.