Difference between revisions of "Manuals/calci/LB"
| (One intermediate revision by the same user not shown) | |||
| Line 11: | Line 11: | ||
*For example, the binary logarithm of 1 is 0, the binary logarithm of 2 is 1, the binary logarithm of 4 is 2, and the binary logarithm of 32 is 5. | *For example, the binary logarithm of 1 is 0, the binary logarithm of 2 is 1, the binary logarithm of 4 is 2, and the binary logarithm of 32 is 5. | ||
*This function will return the result as NaN when the given number as negative. | *This function will return the result as NaN when the given number as negative. | ||
| + | |||
| + | ==Examples== | ||
| + | #LB(20) = 4.321928094887363 | ||
| + | #LB(192) = 7.584962500721156 | ||
| + | #LB(5423) = 12.40487545501521 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=Ampp0Zy6zEw|280|center|Log with base2}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/LOG | LOG]] | ||
| + | *[[Manuals/calci/EXP | EXP]] | ||
| + | *[[Manuals/calci/LN | LN]] | ||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
| + | |||
| + | ==References== | ||
| + | [https://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:55, 14 January 2019
LB (Number)
- is any positive real number.
Description
- This function shows the logarithm value of base 2.
- In , is any positive real number.
- LB means the logarithm with the base 2.
- So the Binary logarithm is the logarithm to the base 2.
- The Binary logarithm function is the inverse function of the power of two function.
- So for any real number x, , .
- For example, the binary logarithm of 1 is 0, the binary logarithm of 2 is 1, the binary logarithm of 4 is 2, and the binary logarithm of 32 is 5.
- This function will return the result as NaN when the given number as negative.
Examples
- LB(20) = 4.321928094887363
- LB(192) = 7.584962500721156
- LB(5423) = 12.40487545501521
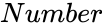 is any positive real number.
is any positive real number.